సున్న

అంకెలు 0 | 1 | 2| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 100 | 108 | 1000 | 1116 ఈ అంకె గురించి
Cardinal	0 zero o/oh nought naught nil null
Ordinal	0th zeroth
Factorization	$0$
Divisors	N/A
Roman numeral	N/A
Japanese numeral	〇
Binary	0
Octal	0
Duodecimal	0
Hexadecimal	0

సున్న ఒక అంకె మరియు ఇతర సంఖ్యలు (పది కంటే పెద్ద సంఖ్యలు, దశమ స్థానాలు) వ్రాయడములో ఉపయోగ పడే అక్షరము కూడా. సున్న అంటే శూన్యము అంటే ఏ విలువ లేకపోవడము. పూర్ణాంకాలు, సహజ సంఖ్యల సంకలనము లో, ఇతర బీజగణిత నిర్మాణాలలో ఐడెంటిటీ^{[తెలుగు పదము కావాలి]} గా ఉపయోగపడుతుంది. స్థానమును నిర్థారించడానికి కూడా సున్న ను వాడతారు. చారిత్రాత్మకంగా సున్న వాడుక లోకి వచ్చిన ఆఖరి అంకె. ఇంగ్లీషులో సున్నని అంకెగా ఉన్నపుడు 'నల్' అని కాని 'నిల్' అని , న్యూమరల్^{[తెలుగు పదము కావాలి]} గ ఉన్నపుడు 'ఓ' అని, నాట్ అని అన్ని పరిస్థితులలో అనపడుతుంది.

ఒక అంకెగా సున్న

ధన 1 ముందు , ఋణ 1 తరువాత సున్న వస్తుంది. చాలా సంఖ్యా వ్యవస్థలలో 0, ఋణ సంఖ్యల కంటే ముందు తీసుకొనబడింది. హైరోగ్లఫిక్స్^{[తెలుగు పదము కావాలి]} లో ధైర్యమైనది అని పిలువబడును.

Zero is a number which quantifies a count or an amount of null size; that is, if the number of your brothers is zero, that means the same thing as having no brothers, and if something has a weight of zero, it has no weight. If the difference between the number of pieces in two piles is zero, it means the two piles have an equal number of pieces. Before counting starts, the result can be assumed to be zero; that is the number of items counted before you count the first item and counting the first item brings the result to one. And if there are no items to be counted, zero remains the final result.

While mathematicians all accept zero as a number, some non-mathematicians would say that zero is not a number, arguing that one cannot have zero of something. Others hold that if one has a bank balance of zero, one has a specific quantity of money in that account, namely none. It is that latter view which is accepted by mathematicians and most others.

Almost all historians omit the year zero from the proleptic Gregorian and Julian calendars, but astronomers include it in these same calendars. However, the phrase Year Zero may be used to describe any event considered so significant that it virtually starts a new time reckoning.

0 as a numeral

The modern numeral 0 is normally written as a circle, ellipse or (rounded) rectangle. In old-style fonts with text figures, 0 is usually the same height as a lowercase x.

Unusual appearance of the digit zero on seven-segment displays

Usual appearance of the digit zero on seven-segment displays

On the seven-segment displays of calculators, watches, etc., 0 is usually written with six line segments, though on some historical calculator models it was written with four line segments. This variant glyph has not caught on.

It is important to distinguish the number zero (as in the "zero brothers" example above) from the numeral or digit zero, used in numeral systems using positional notation. Successive positions of digits have higher values, so the digit zero is used to skip a position and give appropriate value to the preceding and following digits. A zero digit is not always necessary in a positional number system: bijective numeration provides a possible counterexample.

Distinguishing zero from O

A comparison of the letter O and the number 0.

The oval-shaped zero and circular letter O together came into use on modern character displays. The zero with a dot in the centre seems to have originated as an option on IBM 3270 controllers (this has the problem that it looks like the Greek letter Theta). The slashed zero, looking identical to the letter O other than the slash, is used in old-style ASCII graphic sets descended from the default typewheel on the venerable ASR-33 Teletype. This format causes problems because of its similarity to the symbol $\emptyset$, representing the empty set, as well as for certain Scandinavian languages which use Ø as a letter.

The convention which has the letter O with a slash and the zero without was used at IBM and a few other early mainframe makers; this is even more problematic for Scandinavians because it means two of their letters collide. Some Burroughs/Unisys equipment displays a zero with a reversed slash. And yet another convention common on early line printers left zero unornamented but added a tail or hook to the letter-O so that it resembled an inverted Q or cursive capital letter-O.

A german licence plate showing zeroes, this happens to be a plate of an official car

The typeface used on some European number plates for cars distinguish the two symbols by making the zero rather egg-shaped and the O more circular, but most of all by slitting open the zero on the upper right side, so the circle is not closed any more (as in German plates). The typeface chosen is called fälschungserschwerende Schrift (abbr.: FE Schrift), meaning "script which is harder to falsify". Note that those used in the United Kingdom do not differentiate between the two as there can never be any ambiguity if the design is correctly spaced.

In paper writing one may not distinguish the 0 and O at all, or may add a slash across it in order to show the difference, although this sometimes causes ambiguity in regard to the symbol for the null set.

Etymology

The word "zero" came via French zéro from Venetian language zero, which (together with "cipher") came via Italian zefiro from Arabic صفر, şafira = "it was empty", şifr = "zero", "nothing", which was used to translate Sanskrit śūnya ( शून्य ), meaning void or empty.

Italian zefiro already meant "west wind" from Latin and Greek zephyrus; this may have influenced the spelling when transcribing Arabic şifr. The Italian mathematician Fibonacci (c.1170-1250), who grew up in Arab North Africa and is credited with introducing the Hindu decimal system to Europe, used the term zephyrum. This became zefiro in Italian, which was contracted to zero in Venetian, giving the modern English word.

As the Hindu decimal zero and its new mathematics spread from the Arab world to Europe in the Middle Ages, words derived from sifr and zephyrus came to refer to calculation, as well as to privileged knowledge and secret codes. According to Ifrah, "in thirteenth-century Paris, a 'worthless fellow' was called a "... cifre en algorisme", i.e., an "arithmetical nothing"." (Algorithm is also a borrowing from the Arabic, in this case from the name of the 9th century mathematician al-Khwarizmi.) From şifr also came French chiffre = "digit", "figure", "number", chiffrer = "to calculate or compute", chiffré= "encrypted". Today, the word in Arabic is still sifr, and cognates of sifr are common throughout the languages of Europe.

History

Zero appears in the Hindu number system, which is used by all humanity today was developed by 6th century Indian mathematician Brahmagupta. By the mid 2nd millennium BC, the Babylonians had a sophisticated sexagesimal positional numeral system. The lack of a positional value (or zero) was indicated by a space between sexagesimal numerals. By 300 BC a punctuation symbol (two slanted wedges) was co-opted as a placeholder in the same Babylonian system. In a tablet unearthed at Kish (dating from perhaps as far back as 700 BC), the scribe Bêl-bân-aplu wrote his zeroes with three hooks, rather than two slanted wedges.

The Babylonian placeholder was not a true zero because it was not used alone. Nor was it used at the end of a number. Thus numbers like 2 and 120 (2×60), 3 and 180 (3×60), 4 and 240 (4×60), et al., looked the same because the larger numbers lacked a final sexagesimal placeholder. Only context could differentiate them.

Records show that the ancient Greeks seemed unsure about the status of zero as a number: they asked themselves "How can nothing be something?", leading to interesting philosophical and, by the Medieval period, religious arguments about the nature and existence of zero and the vacuum. The paradoxes of Zeno of Elea depend in large part on the uncertain interpretation of zero.

Early use of something like zero by the Indian scholar Pingala (circa 5th-2nd century BC), implied at first glance by his use of binary numbers, is only the modern binary representation using 0 and 1 applied to Pingala's binary system, which used short and long syllables (the latter equal in length to two short syllables), making it similar to Morse code. Nevertheless, he and other Indian scholars at the time used the Sanskrit word śūnya (the origin of the word zero after a series of transliterations and a literal translation) to refer to zero or void.

దస్త్రం:Tres Zapotes Stela.C.back.Pt1.jpg

The back of Stela C from Tres Zapotes, an Olmec archaeological site
This is the second oldest Long Count date yet discovered. The numerals 7.16.6.16.18 translate to September 32 BCE (Julian). The glyphs surrounding the date are what is thought to be one of the few surviving examples of Epi-Olmec script.

History of zero

The Mesoamerican Long Count calendar developed in south-central Mexico required the use of zero as a place-holder within its vigesimal (base-20) positional numeral system. A shell glyph -- -- was used as a zero symbol for these Long Count dates, the earliest of which (on Stela 2 at Chiapa de Corzo, Chiapas) has a date of 36 BCE. Since the eight earliest Long Count dates appear outside the Maya homeland, it is assumed that the use of zero in the Americas predated the Maya and was possibly the invention of the Olmecs. Indeed, many of the earliest Long Count dates were found within the Olmec heartland, although the fact that the Olmec civilization had come to an end by the 4th century BCE, several centuries before the earliest known Long Count dates, argues against the zero being an Olmec discovery.

Although zero became an integral part of Maya numerals, it of course did not influence Old World numeral systems.

By 130, Ptolemy, influenced by Hipparchus and the Babylonians, was using a symbol for zero (a small circle with a long overbar) within a sexagesimal numeral system otherwise using alphabetic Greek numerals. Because it was used alone, not just as a placeholder, this Hellenistic zero was perhaps the first documented use of a number zero in the Old World. However, the positions were usually limited to the fractional part of a number (called minutes, seconds, thirds, fourths, etc.)—they were not used for the integral part of a number. In later Byzantine manuscripts of his Syntaxis Mathematica (Almagest), the Hellenistic zero had morphed into the Greek letter omicron (otherwise meaning 70).

Another zero was used in tables alongside Roman numerals by 525 (first known use by Dionysius Exiguus), but as a word, nulla meaning nothing, not as a symbol. When division produced zero as a remainder, nihil, also meaning nothing, was used. These medieval zeros were used by all future medieval computists (calculators of Easter). An isolated use of their initial, N, was used in a table of Roman numerals by Bede or a colleague about 725, a zero symbol.

In 498 CE, Indian mathematician and astronomer Aryabhata stated that "Sthanam sthanam dasa gunam" or place to place in ten times in value, which may be the origin of the modern decimal based place value notation.

The oldest known text to use zero is the Jain text from India entitled the Lokavibhaaga, dated 458 CE. it was first introduced to the world centuries later by Al Khawarizmim, a Persian mathematician, astronomer and geographer. He was the founder of several branches and basic concepts of mathematics. In the words of Phillip Hitti, Al Khawarizmi's contribution to mathematics influenced mathematical thought to a greater extent. His work on algebra initiated the subject in a systematic form and also developed it to the extent of giving analytical solutions of linear and quadratic equations, which established him as the founder of Algebra. The very name Algebra has been derived from his famous book Al-Jabr wa-al-Muqabilah.

His arithmetic synthesized Greek and Hindu knowledge and also contained his own contribution of fundamental importance to mathematics and science. Thus, he explained the use of zero, a numeral of fundamental importance developed by the Indians. Similarly, he developed the decimal system so that the overall system of numerals, 'algorithm' or 'algorizm' is named after him.

The first indubitable appearance of a symbol for zero appears in 876 in India on a stone tablet in Gwalior. Documents on copper plates, with the same small o in them, dated back as far as the sixth century CE, abound.

Rules of Brahmagupta

The rules governing the use of zero appeared for the first time in Brahmagupta's book Brahmasputha Siddhanta, written in 628. Here Brahmagupta considers not only zero, but negative numbers, and the algebraic rules for the elementary operations of arithmetic with such numbers. In some instances, his rules differ from the modern standard. Here are the rules of Brahamagupta:

• The sum of two positive quantities is positive
• The sum of two negative quantities is negative
• The sum of zero and a negative number is negative
• The sum of zero and a positive number is positive
• The sum of zero and zero is zero.
• The sum of a positive and a negative is their difference; or, if they are equal, zero
• In subtraction, the less is to be taken from the greater, positive from positive
• In subtraction, the less is to be taken from the greater, negative from negative
• When the greater however, is subtracted from the less, the difference is reversed
• When positive is to be subtracted from negative, and negative from positive, they must be added together
• The product of a negative quantity and a positive quantity is negative
• The product of a negative quantity and a negative quantity is positive
• The product of two positive, is positive.
• Positive divided by positive or negative by negative is positive
• Positive divided by negative is negative. Negative divided by positive is negative
• A positive or negative number when divided by zero is a fraction with the zero as denominator
• Zero divided by a negative or positive number is either zero or is expressed as a fraction with zero as numerator and the finite quantity as denominator
• Zero divided by zero is zero.

In saying zero divided by zero is zero, Brahmagupta differs from the modern position. Mathematicians normally do not assign a value, whereas computers and calculators will sometimes assign NaN, which means "not a number." Moreover, non-zero positive or negative numbers when divided by zero are either assigned no value, or a value of unsigned infinity, positive infinity, or negative infinity. Once again, these assignments are not numbers, and are associated more with computer science than pure mathematics, where in most contexts no assignment is made. (See division by zero)

Zero as a decimal digit

See also: History of the Hindu-Arabic numeral system.

Positional notation without the use of zero (using an empty space in tabular arrangements, or the word kha "emptiness") is known to have been in use in India from the 6th century. The earliest certain use of zero as a decimal positional digit dates to the 9th century. The glyph for the zero digit was written in the shape of a dot, and consequently called bindu ("dot").

The Hindu numeral system(base 10) reached Europe in the 11th century, via the Iberian Peninsula through Spanish Muslims the Moors, together with knowledge of astronomy and instruments like the astrolabe, first imported by Gerbert of Aurillac. So in Europe they came to be known as "Arabic numerals". The Italian mathematician Fibonacci or Leonardo of Pisa was instrumental in bringing the system into European mathematics in 1202, stating:

After my father's appointment by his homeland as state official in the customs house of Bugia for the Pisan merchants who thronged to it, he took charge; and in view of its future usefulness and convenience, had me in my boyhood come to him and there wanted me to devote myself to and be instructed in the study of calculation for some days. There, following my introduction, as a consequence of marvelous instruction in the art, to the nine digits of the Hindus, the knowledge of the art very much appealed to me before all others, and for it I realized that all its aspects were studied in Egypt, Syria, Greece, Sicily, and Provence, with their varying methods; and at these places thereafter, while on business. I pursued my study in depth and learned the give-and-take of disputation. But all this even, and the algorism, as well as the art of Pythagoras, I considered as almost a mistake in respect to the method of the Hindus (Modus Indorum). Therefore, embracing more stringently that method of the Hindus, and taking stricter pains in its study, while adding certain things from my own understanding and inserting also certain things from the niceties of Euclid's geometric art. I have striven to compose this book in its entirety as understandably as I could, dividing it into fifteen chapters. Almost everything which I have introduced I have displayed with exact proof, in order that those further seeking this knowledge, with its pre-eminent method, might be instructed, and further, in order that the Latin people might not be discovered to be without it, as they have been up to now. If I have perchance omitted anything more or less proper or necessary, I beg indulgence, since there is no one who is blameless and utterly provident in all things. The nine Indian figures are: 9 8 7 6 5 4 3 2 1. With these nine figures, and with the sign 0 ... any number may be written.

Here Leonardo of Pisa uses the word sign "0", indicating it is like a sign to do operations like addition or multiplication, but he did not recognize zero as a number on its own right. From the 13th century, manuals on calculation (adding, multiplying, extracting roots etc.) became common in Europe where they were called algorimus after the Persian mathematician al-Khwarizmi. The most popular was written by John of Sacrobosco about 1235 and was one of the earliest scientific books to be printed in 1488. Hindu-Arabic numerals until the late 15th century seem to have predominated among mathematicians, while merchants preferred to use the abacus. It was only from the 16th century that they became common knowledge in Europe.

In mathematics

Elementary algebra

Zero (0) is the least non-negative integer. The natural number following zero is one and no natural number precedes zero. Zero may or may not be counted as a natural number, depending on the definition of natural numbers.

In set theory, the number zero is the cardinality of the empty set: if one does not have any apples, then one has zero apples. In fact, in certain axiomatic developments of mathematics from set theory, zero is defined to be the empty set. When this is done, the empty set is the Von Neumann cardinal assignment for a set with no elements, which is the empty set. The cardinality function, applied to the empty set, returns the empty set as a value, thereby assigning it zero elements.

Zero is neither positive nor negative, neither a prime number nor a composite number, nor is it a unit. If zero is excluded from the rational numbers, the real numbers or the complex numbers, the remaining numbers form an abelian group under multiplication.

The following are some basic rules for dealing with the number zero. These rules apply for any complex number x, unless otherwise stated.

• Addition: x + 0 = 0 + x = x. That is, 0 is an identity element (or neutral element) with respect to addition.
• Subtraction: x − 0 = x and 0 − x = − x.
• Multiplication: x · 0 = 0 · x = 0.
• Division: 0 / x = 0, for nonzero x. But x / 0 is undefined, because 0 has no multiplicative inverse, a consequence of the previous rule. For positive x, as y in x / y approaches zero from positive values, its quotient increases toward positive infinity, but as y approaches zero from negative values, the quotient increases toward negative infinity. It is said that x / 0 equals unsigned infinity, see division by zero.
• Exponentiation: x⁰ = 1, except that the case x = 0 may be left undefined in some contexts. For all positive real x, 0^x = 0.

The expression "0/0" is an "indeterminate form". That does not simply mean that it is undefined; rather, it means that if f(x) and g(x) both approach 0 as x approaches some number, then f(x)/g(x) could approach any finite number or ∞ or −∞; it depends on which functions f and g are. See l'Hôpital's rule.

The sum of 0 numbers is 0, and the product of 0 numbers is 1.

Extended use of zero in mathematics

• Zero is the identity element in an additive group or the additive identity of a ring.
• A zero of a function is a point in the domain of the function whose image under the function is zero. When there are finitely many zeros these are called the roots of the function. See zero (complex analysis).
• In geometry, the dimension of a point is 0.
• The concept of "almost" impossible in probability. More generally, the concept of almost nowhere in measure theory. For instance: if one chooses a point on a unit line interval [0,1) at random, it is not impossible to choose 0.5 exactly, but the probability that you will is zero.
• A zero function (or zero map) is a constant function with 0 as its only possible output value; i.e., f(x) = 0 for all x defined. A particular zero function is a zero morphism in category theory; e.g., a zero map is the identity in the additive group of functions. The determinant on non-invertible square matrices is a zero map.
• Zero is one of three possible return values of the Möbius function. Passed an integer of the form x² or x²y (for x > 1), the Möbius function returns zero.
• Zero is the first Perrin number.

In science

Physics

The value zero plays a special role for a large number of physical quantities. For some quantities, the zero level is naturally distinguished from all other levels, whereas for others it is more or less arbitrarily chosen. For example, on the kelvin temperature scale, zero is the coldest possible temperature (negative temperatures exist but are not actually colder), whereas on the celsius scale, zero is arbitrarily defined to be at the freezing point of water. Measuring sound intensity in decibels or phons, the zero level is arbitrarily set at a reference value—for example, at a value for the threshold of hearing. See also Zero-point energy.

Chemistry

Zero has been proposed as the atomic number of the theoretical element tetraneutron. It has been shown that a cluster of four neutrons may be stable enough to be considered an atom in their own right. This would create an element with no protons and no charge on its nucleus.

As early as 1926 Professor Andreas von Antropoff coined the term neutronium for a conjectured form of matter made up of neutrons with no protons, which he placed as the chemical element of atomic number zero at the head of his new version of the periodic table. It was subsequently placed as a noble gas in the middle of several spiral representations of the periodic system for classifying the chemical elements. It is at the centre of the Chemical Galaxy (2005).

In computer science

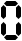
Numbering from 1 or 0?

The most common practice throughout human history has been to start counting at one. Nevertheless, in computer science zero has become the standard starting point. For example, in almost all old programming languages, an array starts from 1 by default. As programming languages have developed, it has become more common that an array starts from zero by default, the "first" item in the array being item 0. In particular, the popularity of the programming language "C" in the 1980s has made this approach common.

One reason for this convention is that modular arithmetic normally describes a set of N numbers as containing 0,1,2,...N-1 in order to contain the additive identity. Because of this, many arithmetic concepts (such as hash tables) are less elegant to express in code unless the array starts at zero.

A second reason to use zero-based array indices is that this can improve efficiency under certain circumstances. To illustrate, suppose a is the memory address of the first element of an array, and i is the index of the desired element. In this fairly typical scenario, it is quite common to want the address of the desired element. If the index numbers count from 1, the desired address is computed by this expression:

$a+s\times (i-1)\,\!$

where s is the size of each element. In contrast, if the index numbers count from 0, the expression becomes this:

$a+s\times i\,\!$

This simpler expression can be more efficient to compute in certain situations.

Note, however, that a language wishing to index arrays from 1 could simply adopt the convention that every "array address" is represented by $a'=a-s$; that is, rather than using the address of the first array element, such a language would use the address of an imaginary element located immediately before the first actual element. The indexing expression for a 1-based index would be the following:

$a'+s\times i\,\!$

Hence, the efficiency benefit of zero-based indexing is not inherent, but is an artefact of the decision to represent an array by the address of its first element.

A third reason is that ranges are more elegantly expressed as the half-open interval, $[0,n)$, as opposed to the closed interval, $[1,n]$, because empty ranges often occur as input to algorithms (which would be tricky to express with the closed interval without resorting to obtuse conventions like $[1,0]$). On the other hand, closed intervals occur in mathematics because it's often necessary to calculate the terminating condition (which would be impossible in some cases because the half-open interval isn't always a closed set) which would have a subtraction by 1 everywhere.

This situation can lead to some confusion in terminology. In a zero-based indexing scheme, the first element is "element number zero"; likewise, the twelfth element is "element number eleven". Therefore, an analogy from the ordinal numbers to the quantity of objects numbered appears; the highest index of n objects will be (n-1) and referred to the n:th element. For this reason, the first element is often referred to as the zeroth element to eliminate any possible doubt (though, strictly speaking, this is unnecessary and arguably incorrect, since the meanings of the ordinal numbers are not ambiguous).

Null value

In databases a field can have a null value. This is equivalent to the field not having a value. For numeric fields it is not the value zero. For text fields this is not blank nor the empty string. The presence of null values leads to three-valued logic. No longer is a condition either true or false, but it can be undetermined. Any computation including a null value delivers a null result. Asking for all records with value 0 or value not equal 0 will not yield all records, since the records with value null are excluded.

Null pointer

A null pointer is a pointer in a computer program that does not point to any object or function. In C, the integer constant 0 is converted into the null pointer at compile time when it appears in a pointer context, and so 0 is a standard way to refer to the null pointer in code. However, the internal representation of the null pointer may be any bit pattern (possibly different values for different data types), and has no particular association with zero.

(Note that on most common architectures, the null pointer is represented internally by the integer 0, so C compilers on such systems perform no actual conversion).

Negative zero

Because of $-0=0=+0$, both -0 and +0 represent the exact same number in mathematics and there is no “negative zero” distinct from zero. But in some signed number representations (but not the two's complement representation predominant today) and most floating point number representations, zero has two distinct representations, one grouping it with the positive numbers and one with the negatives; this latter representation is known as negative zero. Representations with negative zero can be troublesome, because the two zeros will compare equal but may be treated differently by some operations.

In other fields

International maritime signal flag for 0

• In some countries, dialing 0 on a telephone places a call for operator assistance.
• In Braille, the numeral 0 has the same dot configuration as the letter J.
• DVDs that can be played in any region are sometimes referred to as being "region 0"
• In classical music, 0 is very rarely used as a number for a composition, the only two examples on the fringes of the standard repertoire probably being Anton Bruckner's Symphony No. 0 in D minor and Alfred Schnittke's Symphony No. 0
• In tarot, card No. 0 is the Fool
• In cricket, a player being dismissed having scored no runs is considered to be "out for a duck". This term is derived from the fact that the digit 0 looked like a duck's egg.

Quotes

The importance of the creation of the zero mark can never be exaggerated. This giving to airy nothing, not merely a local habitation and a name, a picture, a symbol, but helpful power, is the characteristic of the Hindu race from whence it sprang. It is like coining the Nirvana into dynamos. No single mathematical creation has been more potent for the general on-go of intelligence and power. G.B. Halsted

...a profound and important idea which appears so simple to us now that we ignore its true merit. But its very simplicity and the great ease which it lent to all computations put our arithmetic in the first rank of useful inventions. Pierre-Simon Laplace

The point about zero is that we do not need to use it in the operations of daily life. No one goes out to buy zero fish. It is in a way the most civilized of all the cardinals, and its use is only forced on us by the needs of cultivated modes of thought. Alfred North Whitehead

...a fine and wonderful refuge of the divine spirit--almost an amphibian between being and non-being. Gottfried Leibniz

References

This article is based on material taken from the Free On-line Dictionary of Computing prior to 1 November 2008 and incorporated under the "relicensing" terms of the GFDL, version 1.3 or later.

• Barrow, John D. (2001) The Book of Nothing, Vintage. ISBN 0-09-928845-1.
• Diehl, Richard A. (2004) The Olmecs: America's First Civilization, Thames & Hudson, London.
• Ifrah, Georges (2000) The Universal History of Numbers: From Prehistory to the Invention of the Computer, Wiley. ISBN 0-471-39340-1.
• Kaplan, Robert (2000) The Nothing That Is: A Natural History of Zero, Oxford: Oxford University Press.
• Seife, Charles (2000) Zero: The Biography of a Dangerous Idea, Penguin USA (Paper). ISBN 0-14-029647-6.

See also

• Negative and non-negative numbers
• Nothing
• Null
• Number theory
• Slashed zero
• Nullar
• Division by zero
• 00

External links

• A History of Zero
• Zero Saga
• The Discovery of the Zero
• The History of Algebra
• Why numbering should start at zero by Edsger Dijkstra
• Numbering Starts with Zero same topic as Dijkstra's article, including some more aspects
• "Zeroes" Song parody
• "My Hero Zero" Educational children's song