కటపయాది పద్ధతి

సంఖ్యలను, పదాలద్వారానూ, శ్లోకాలద్వారానూ సులువుగా గుర్తుపెట్టుకోవడానికి వాడిన ఒక ప్రాచీన భారతీయ విధానం, కటపయాది పద్ధతి. కొన్ని అక్షరాలకు ఒకే లేదా వేర్వేరు అంకెలను కేటాయించి, మరికొన్నిటి విలువని సున్నాగా నిర్ణయించి, అర్థవంతమైన పదాలను సృష్టించి, తద్వారా సంక్లిష్టమైన సంఖ్యలను గుర్తుపెట్టుకోగలగడం, ఈ కటపయాది యొక్క ప్రత్యేకత.
చరిత్ర
[మార్చు]ఈ పద్ధతిని గురించిన అత్యంత ప్రాచీనమైన ఉల్లేఖనం, సా.శ. 683నాటి హరిదత్తుని గ్రహచారణిబంధనం లోనిది.[1] సా.శ. 869నాటి, శంకరనారాయణ రాసిన, లఘుభాష్యకారియవివరణంలో కూడా దీనినివాడినట్టు తెలుస్తోంది.[2] కేరళలో ప్రసిద్ధమైన, కొన్ని ఖగోళ ఉల్లేఖనాలలోని, గ్రహస్థితులు కటపయాది పద్ధతిలో కూర్చబడి ఉన్నాయి. అటువంటి ఉల్లేఖనాలలో మొట్టమొదటిది, వరరుచి వ్రాసిన "చంద్ర వాక్యాని"అని భావిస్తారు. అందువలన కొంతమంది, ఈ పద్ధతికి వరరుచి ఆద్యుడు అని భావిస్తారు.[3] వరరుచి సా.శ. 4 వ శతాబ్దికి చెందినవాడు. అందువలన ఈ పద్ధతి మొదటి సహస్రాబ్దపు తొలి శతాబ్దాలలో పుట్టిందని భావించవచ్చు.[4] ఆర్యభటుని ఆర్యభటీయం లో కూడా ఖగోళ సంఖ్యలను తెలుపడానికి కటపయాది పద్ధతిని వాడినారు. అయితే, ఈ వాడుక మరికొంత ఆధునికతని సంతరించుకొంది.[5]
వాడుక యొక్క భౌగోళికత
[మార్చు]కటపయాది పద్ధతిని ఎక్కువగా దక్షిణ భారతదేశంలో, ప్రముఖంగా కేరళలో వాడినట్లు భావిస్తున్నారు. అయితే, బర్మా దేశంలో కటపయాది పద్ధతిన కొన్ని పాళీ చంద్రసెంగకళలు(Chronogram)లు లభ్యమయ్యాయి. అందువలన ఈ పద్ధతి కేవలం భారతదేశానికే పరిమితం కాలేదని తెలుస్తోంది.[6] అంతేగాక, ఉత్తరభారతదేశంలో లభ్యమైన ఒక సంస్కృత తారేక్షం (Astrolabe)పైన, కటపయాది పద్ధతిలో వివిధ ఎత్తులు, మార్కు చేయబడినట్టు గుర్తించారు. ఇది ప్రస్తుతం, వారణాసిలోని సంపూర్ణానంద విశ్వవిద్యాలయంలో, సరస్వతీ భవన్ గ్రంథాలయంలో ఉన్నది.[1]
నియమాలు
[మార్చు]శంకరవర్మ రాసిన సద్రత్నమాల లోని ఈ క్రింది శ్లోకం, ఈ పద్ధతిని వివరిస్తుంది.[7][8]
నజ్ఞావచశ్చ శూన్యాని సంఖ్యా: కటపయాదయ:|
మిశ్రే తూపాన్త్యహల్ సంఖ్యా న చ చిన్త్యో హలస్వర:||
అనగా, 'న', 'ఞ', , అచ్చులకు "సున్నా" విలువ ఇవ్వబడుతుంది. కటపయతో మొదలు అన్ని హల్లులకు 1-9 వరకూ విలువలివ్వబడ్డాయి. సంయుక్త అక్షరాలు (వత్తులతో సహా) వచ్చినపుడు, వెనుక వచ్చిన హల్లుని మాత్రమే లెక్కలోకి తీసుకోవాల్సి ఉంటుంది. పొల్లు అక్షరాలను విడిచిపెట్టాలి.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
|---|---|---|---|---|---|---|---|---|---|
| ka క | kha ఖ | ga గ | gha ఘ | nga ఙ | ca చ | cha ఛ | ja జ | jha ఝ | nya ఞ |
| ṭa ట | ṭha ఠ | ḍa డ | ḍha ఢ | ṇa ణ | ta త | tha థ | da ద | dha ధ | na న |
| pa ప | pha ఫ | ba బ | bha భ | ma మ | - | - | - | - | - |
| ya య | ra ర | la ల | va వ | śha శ | sha ష | sa స | ha హ | - | - |
- హల్లులకు పై పట్టికలో చూపిన విధంగా విలువలివ్వబడ్డాయి. ఉదాహరణకి, "బ" విలువ ఎప్పుడైనా "3" మాత్రమే, కానీ ఙ, ణ, మ, శ లలో దేనిద్వారానైనా సూచించవచ్చు.
- ఒంటరిగా వచ్చే ఏ అచ్చుకైనా విలువ "0"అవుతుంది.
- సంయుక్తాక్షరాలు లేదా వత్తులతో కూడిన అక్షరాలు ఉన్నప్పుడు అచ్చులతో కూడని హల్లుకి విలువ ఉండదు. ఉదాహరణకి, "క్య" అనే సంయుక్తాక్షరం, ("క్య = క్ + య్ + అ") లో, "య" అచ్చుతో కూడినదై ఉన్నందువలన దాని విలువ మాత్రమే గణించాలి.
- దశాంశ బిందువు వాడకం లేదు.
- భారతీయులు హిందూ-అరబిక్ సంఖ్యలను వాడారు. సాంప్రదాయికంగా, ఈ సంఖ్యలలో ఎడమనుండి కుడికి పోయినపుడు, స్థానవిలువ పెరుగుతుంది. ఇది, "అంకానామ్ వామతో గతి" అనే నియమం మీద ఆధారపడినట్టిది. ఉదాహరణకి, పందొమ్మిది వందల నలభై యేడుని 7491 అని రాయాలి. (1947 అని ఆధునిక ప్రపంచ వాడుక) [9]
తేడాలు
[మార్చు]- ద్రావిడ భాషలలో కనిపించే "ళ" అక్షరం కూడా కొన్నిచోట్ల వాడబడింది.
- కొంతమంది ఒంటరిగా వచ్చే అచ్చులకి "సున్నా"గా పరిగణించరు. విలువలేనివిగా గణిస్తారు.
వాడుక
[మార్చు]గణితం , ఖగోళశాస్త్రాలు
[మార్చు]- సా.శ. 950 ప్రాంతానికి చెందిన రెండవ ఆర్యభట్టుని, "మహా ఆర్య సిద్ధాంతం"లో వృత్త వ్యాసానికీ, దాని చుట్టుకొలతకీ ఉన్న నిష్పత్తి అనగా "పై" () విలువ ఈ క్రింది శ్లోకం క్రోడీకరించబడింది.[10]
గోపీ భాగ్య మధువ్రాత శృఞ్గి శోదరి సంధిగ|
ఖల జీవిత ఖాతావగల హాలార సంధర ||
ఈ పద్యాన్ని కృష్ణుడి పరంగాను, శివుడి పరంగాను కూడా చెప్పుకోవచ్చని భావిస్తారు.
కటపయాది పద్ధతిలో హల్లుల విలువలని పై పద్యంలో అక్షరాలకి వర్తింపజేస్తే వచ్చే సంఖ్య.
3141592653589793 (మొదటి పాదం)
2384626433832792 (రెండవ పాదం)
ఇది పై విలువ (31 దశాంశాల వరకూ) =3.1415926535897932384626433832795...
- కేరళకు చెందిన 14వ శతాబ్దపు గణితవేత్త - జ్యోతిష్కుడు, మాధవుని సైన్ పట్టిక వివిధ కోణాల సైన్ విలువలు ఈ పద్ధతిలోనే సూచించబడ్డాయి.
- 15వ శతాబ్దానికి చెందిన కరణపద్ధతి'లో ', "పై" () విలువ ఈ శ్లోకం సూచిస్తుంది.
అనూననూన్నానననున్ననిత్యై-
స్సమాహతాశ్చక్రకలావిభక్తాః
చండాంశుచంద్రాధమకుంభిపాలైర్-
వ్యాసస్తదర్ద్ధం త్రిభమౌర్విక స్యాత్
- ఇది "అనూననూన్నానననున్ననిత్యై"' (10,000,000,000) వ్యాసంగాగల వృత్తం యొక్క చుట్టుకొలత చండాంశుచంద్రాధమకుంభిపాలైర్"' (31415926536) అనే అర్థం ఇస్తుంది.
- శంకరవర్మ రాసిన సద్రత్నమాల నుండి ఒక ప్రసిద్ధ శ్లోక భాగం కింద ఇవ్వబడింది.
భద్రామ్బుద్ధిసిద్ధజన్మగణితశ్రద్ధా స్మ యద్ భూపగీ:
- ఈ కటపయాది పద్ధతినుపయోగిస్తే,
| భ bha | ద్ d | రా rā | మ్ ṃ | బు ba | ద్ d | ధి dh | సి sa | ద్ d | ధ dha | జ ja | న్ n | మ ma | గ ga | ణి ṇa | త ta | శ్ ṣ | ర ra | ద్ d | ధా dha | స్ s | మ ma | య ya | ద్ d | భూ bha | ప pa | గి gi |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | - | 2 | - | 3 | - | 9 | 7 | - | 9 | 8 | - | 5 | 3 | 5 | 6 | - | 2 | - | 9 | - | 5 | 1 | - | 4 | 1 | 3 |
- ఇది సాంప్రదాయికంగా ఉన్న వరుస అయినందువలన, ఈ సంఖ్యని వెనుకనుండి రాస్తే "314159265358979324" వస్తుంది. ఇది పై (π) విలువని 17 దశాంశాల వరకూ ఇస్తుంది.
కర్ణాటక సంగీతం
[మార్చు]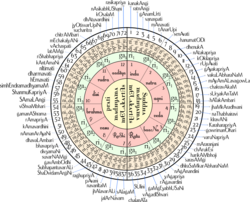
కర్ణాటక సంగీతంలోని, జనక రాగాలను క్రమపద్ధతిలో పొందుపరచి, ప్రతీ రాగానికీ ఒక సంఖ్యని కేటాయించారు. ఈ సంఖ్యని మేళకర్త సంఖ్య అని కూడా అంటారు. కర్ణాటక సంగీతంలో మేళకర్త రాగాలు లేదా సంపూర్ణ రాగాలు లేదా జనక రాగాలు మొత్తం 72 ఉన్నాయి. ఈ రాగాలలోని మొదటి రెండు అక్షరాలు, (కటపయాది పద్ధతిలో) ఆ రాగం యొక్క క్రమసంఖ్యని సూచిస్తాయి. అనంతమైన జన్య రాగాలు ఈ మేళకర్త రాగాల నుండే జనించాయి. మేళ కర్త సంఖ్యని ఉపయోగించి, రాగాలలో స్వరాల క్రమాన్ని పొందవచ్చును.
- "స" "ప" స్వరాలు స్థిరములు
- 1 నుండి 36 వరకూ మేళకర్త రాగాలలో "మ1" ఉంటుంది, 37 నుండి 72 వరకూ "మ2" ఉంటుంది.
- ఇతర స్వరక్రమాన్ని, మేళకర్త సంఖ్యని ఒక్క విలువ తగ్గించి, పిమ్మట 6 తో భాగింపగా వచ్చిన భాగఫలం, శేషాల ఆధారంగా కనుగొనవచ్చును.
- "రి", "గ" స్థానాలలో
- "రి1", "గ1" (భాగఫలం 0 అయినపుడు)
- "రి1", "గ2" (భాగఫలం 1 అయినపుడు)
- "రి1", "గ3" (భాగఫలం 2 అయినపుడు)
- "రి2", "గ2" (భాగఫలం 3 అయినపుడు)
- "రి2", "గ3" (భాగఫలం 4 అయినపుడు)
- "రి3", "గ3" (భాగఫలం 5 అయినపుడు)
ఉంటాయి.
- "ద", "ని" స్థానాలలో
- "ద1", "ని1" (శేషం 0 అయినపుడు)
- "ద1", "ని2" (శేషం 1 అయినపుడు)
- "ద1", "ని3" (శేషం 2 అయినపుడు)
- "ద2", "ని2" (శేషం 3 అయినపుడు)
- "ద2", "ని3" (శేషం 4 అయినపుడు)
- "ద3", "ని3" (శేషం 5 అయినపుడు)
ఉదాహరణ,
- ధీరశంకరాభరణం రాగం
కటపయాది పద్ధతిలో, ధ 9, ర 2, ఆధునికవాడుక ప్రకారం, 92 29 ఇది, శంకరాభరణం రాగం యొక్క మేళకర్త సంఖ్య. ఇది 36 కన్నా తక్కువ కనుక 'మ1' ఉంటుంది. 29ని ఒక్క విలువ తగ్గిస్తే 28 అవుతుంది. 6 తో 28ని భాగింపగా భాగపలం 4, శేషం 4 . అందువలన ఈ రాగం యొక్క స్వరక్రమం, స రి2 గ3 మ1 ప ద2 ని3 స'.
- మేచ కళ్యాణి రాగం
కటపయాది పద్ధతిలో, మ 5, చ 6, ఆధునికవాడుక ప్రకారం, 56 65 ఇది, మేచ కళ్యాణిరాగం యొక్క మేళకర్త సంఖ్య. ఇది 36 కన్నా ఎక్కువ కనుక 'మ2' ఉంటుంది. 65 నుండి 36ని తీసివేస్తే 29. 29నుండి ఒక్క విలువ తగ్గిస్తే 28 అవుతుంది. 6 తో 28ని భాగింపగా భాగపలం 4, శేషం 4 . అందువలన ఈ రాగం యొక్క స్వరక్రమం, స రి2 గ3 మ2 ప ద2 ని3 స'.
- సింహేద్రమధ్యమం రాగం
కటపయాది పద్ధతిలో, స 7, హ 8, ఆధునికవాడుక ప్రకారం, 78 87 అనిపిస్తంది. కానీ, ఇది నిజానికి సిహ్మేంద్రమధ్యమం అని వ్రాయబడిందని, ఎక్కువమంది భావిస్తారు (ఉచ్చారణలో మార్పు ఉండదు). అప్పుడు కటపయాది పద్ధతిలో, స 7, మ 5, ఆధునికవాడుక ప్రకారం, 75 57 అవుతుంది. ఇది, సిహ్మేంద్ర మధ్యమం రాగం యొక్క మేళకర్త సంఖ్య. ఇది 36 కన్నా ఎక్కువ కనుక 'మ2' ఉంటుంది. 57 నుండి 36ని తీసివేస్తే 21, 21ని ఒక్క విలువ తగ్గిస్తే 20 అవుతుంది. 6 తో 20ని భాగింపగా భాగపలం 3, శేషం 2 . అందువలన ఈ రాగం యొక్క స్వరక్రమం, స రి2 గ2 మ2 ప ద1 ని3 స'.
తేదీలు సూచించడం
[మార్చు]ముఖ్యమైన తేదీలు కటపయాది పద్ధతినుపయోగించి గుర్తుపెట్టుకునేవారు. సాధారణంగా, ఈ లెక్కింపు కలియుగంలో ఆ తేదీ ఎన్నవ రోజు అనే దానినే ఉపయోగించేవారు.
- ప్రస్తుత మలయాళం కేలండరు (కొల్లవర్షం అని పిలుస్తారు), అంతకు ముందున్న కేలండర్ల స్థానంలో సా.శ. 825 నుండి అనుసరించబడుతోంది. ఆ రోజుని, "ఆచార్య వాగ్బాధా"గా గుర్తుంచుకున్నారు. ఈ పద్ధతి ప్రకారం, ఆ రోజు, కలియుగం మొదలైన పిమ్మట 1434160వరోజు.[11]
- మేల్పతూర్ నారాయణ భట్టాద్రి రాసిన నారాయణీం, "ఆయురారోగ్యసౌఖ్యమ్" అనే వాక్యంతో ముగుస్తుంది. కటపయాది ప్రకారం, దీని విలువ "1712210". ఇది ఆ రచన పూర్తయిన రోజు. (కలి శకం) [12]
ఇతరములు
[మార్చు]- కొంతమంది, పుట్టినపిల్లలకి పేర్లు పెట్టడానికి కూడా ఈ పద్ధతిని వాడతారు.[13][14]
- కోడునల్లూరు కున్నికుట్టన్ తంబూరన్, కటపయాది పద్ధతి ఉపయోగించి, మలయాళంలో రాసిన ఈ వాక్యం గ్రెగొరియన్ కేలండరులోని నెలలను గుర్తుపెట్టుకోడానికి ఉద్దేశించింది.
- పలహారే పాలు నల్లూ, పులర్న్నాలో కలక్కిలాం
- ఇల్లా పాలెన్ను గోపాలన్ - ఆంగ్లమాసదినం క్రమాల్
దీనర్థం, "ఉదయాహారానికి పాలు మంచివి, పొద్దన్న, వాటిని చిలుకుకోవాలి. కానీ, గోపాలన్ పాలు లేవన్నాడు."
"కటపయాది" ద్వారా దీనిని అంకెలలో మారిస్తే, పల = 31, హారే = 28, పాలు = 31, నల్లూ = 30, పులర్ = 31, న్నాలో = 30, కల = 31, క్కిలాం = 31, ఇల్లా =30, పాలే = 31, న్ను గో = 30, పాలన్ = 31.
ఇవి కూడా చూడండి
[మార్చు]మూలాలు
[మార్చు]- ↑ 1.0 1.1 Sreeramamula Rajeswara Sarma (1999). "Kaṭapayādi Notation on a Sanskrit Astrolabe" (PDF). Retrieved 2020-07-11.
- ↑ O'Connor, J J; Robertson, E F (1 November 2000). "Sankara Narayana". School of Mathematics and Statistics, University of St Andrews, Scotland. Retrieved 1 January 2010.
- ↑ Usenet Discussion. "Aryabhatta's numerical encoding". Archived from the original on 17 జూలై 2011. Retrieved 1 January 2010.
- ↑ Plofker, Kim (2008). Mathematics in India. Princeton University Press. p. 384. ISBN 978-0-691-12067-6.
- ↑ Fleet, J. F. "The Ka-ta-pa-ya-di Notation of the Second Arya-Siddhanta". The Journal of the Royal Asiatic Society of Great Britain and Ireland. Royal Asiatic Society of Great Britain and Ireland: 459–462. JSTOR 25190035.
- ↑ J.F. Fleet (1911-07-01). "The Katapayadi System of Expressing Numbers". The Journal of the Royal Asiatic Society of Great Britain and Ireland. Royal Asiatic Society of Great Britain and Ireland: 788–794. JSTOR 25189917.
- ↑ K. V. Sarma (2001). ""Sadratnamala of Sankara Varman"" (PDF). Indian Journal of History of Science (Indian National Academy of Science, New Delhi). pp. 1–58. Archived from the original (PDF) on 2015-04-02.
- ↑ Anand Raman, The Ancient Katapayadi Formula and the Modern Hashing Method [1] Archived 2011-06-16 at the Wayback Machine
- ↑ "Aryabhatta's Numerical Encoding". Archived from the original on 2011-07-17. Retrieved 2011-07-17.
- ↑ "శాస్త్ర విజ్ఞానం బ్లాగు, శ్రీనివాస చక్రవర్తి". Archived from the original on 2016-03-07. Retrieved 2013-01-17.
- ↑ Francis Zimmerman, 1989, Lilavati, gracious lady of arithmetic - India - A Mathematical Mystery Tour [2]
- ↑ Dr. C Krishnan Namboodiri, Chekrakal Illam, Calicut, Namboothiti.com Dr. C Krishnan Namboodiri. ""Katapayaadi" or "Paralpperu"". Namboothiri Websites Trust. Retrieved 1 January 2010.
- ↑ Visti Larsen, Choosing the auspicious name[permanent dead link]
- ↑ [3]


