ఫారడే ప్రేరణ నియమం

ఒక వాహకం సమయంతో మరో అయస్కాంత క్షేత్రమునకు బహిర్గతం అయినప్పుడు దాని గుండా వోల్టేజ్ ఉత్పత్తి అవుతుంది. దీనినే విద్యుదయస్కాంత ప్రేరణ అని అంటారు. ఈ ఆవిష్కరణకు గుర్తింపు మైఖేల్ ఫారడేకు 1831 సం.లో దక్కింది. జోసెఫ్ హెన్రి కూడా ఇలాంటి ఆవిష్కరణ చేసినప్పటికీ ఆయన ఎటువంటి ప్రచురణ చేయలేదు. ఫారడే ప్రేరణ నియమం విద్యుదయస్కాంత శక్తి యొక్క మూల నియమం. ఇది ఒక విద్యుద్వలయం ఎలెక్త్రోమోటివ్ శక్తి (ఈఎమ్‌ఎఫ్) ని ఉత్పత్తి చేయుటకు అయస్కాంత రంగంతో ఎలా ప్రతిస్పందిస్తుందో చెప్తుంది. ఇది ట్రాన్స్ఫోర్మర్, ఇండక్టర్, వివిధ రకాల విద్యుత్ మోటర్లు, జెనరేటర్లు, సోలెనోయిడ్ల యొక్క మూల కార్యాచరణ నియమం.^[1]^[2] మాక్స్వెల్ల్- ఫారడే సమీకరణం అనునది ఫారడే నియమం యొక్క సర్వ సమన్వయం, మాక్స్వెల్ల్ సమీకరణములలో ఒకటి.

చరిత్ర

ఫారడే, జోసెఫ్ హెన్రి ఇరువురూ కూడా విద్యుదయస్కాంత ప్రేరణను 1831^[4]లో స్వతంత్రముగా కనుగొన్నారు. అయినప్పటికి ఫారడే తన పరిశోధనల ఫలితాలను మొదట ప్రచురించారు^[5].^[6] ఫారడే యొక్క మొదటి విద్యుదయస్కాంత ప్రేరణ ప్రయోగ నిరూపణలో ఇనుప వలయం లేదా టోరూస్ యొక్క ఎదురెదురుగా ఉండే భుజాల చుట్టూ రెండు తీగలు చుట్టాడు. (ఒక ఆధునిక టోరోయిడల్ ట్రాన్స్ఫార్మర్ ను పోలివున్న అమరిక.) ఆయన ఇటీవల కనుగొన్న విద్యుదయస్కాంతుల లక్షణాల ఆధారంగా, ఎప్పుడైతే కరెంట్ ఒక తీగలో ప్రవహించడం మొదలవుతుందో అప్పుడు ఒక రకమైన తరంగము తీగ గుండా ప్రవహించి అవతలి వైపు ఒక రకమైన విద్యుత్ ప్రబావ౦ ను కలిగిస్తుందని ఊహించారు.ఆయన ఒక తీగను గల్వనోమీటర్ కు ఇంకొక తీగను బ్యాటరీకు కనెక్ట్ చేసి చూసారు.నిజానికి ఆయన కనెక్ట్ చేసినప్పుడు ఒకటి, కనెక్షన్ తీసినప్పుడు ఇంకొక తాత్కాలిక విద్యుత్తు ప్రవాహన (ఆయన దీనిని విద్యుత్తు యొక్క తరంగం అని అన్నారు) ను గమనించారు.ఈ ప్రేరణకు కారణం బ్యాటరీ కనెక్ట్, డిస్కోన్నెక్ట్ చేసినప్పుడు సంభవించిన అయస్కాంత ధార లోని మార్పు . ఇంకో రెండు నెలలోనే ఫారడే విద్యుదయస్కాంత ప్రేరణ యొక్క మరెన్నో వ్యక్తీకరణలను కనుగొన్నారు^[7].ఆయన ఒక బార్ అయస్కాంతాన్ని తీగల వేష్టం లోపలికి, బయటికి జరపడం వల్ల తాత్కాలిక కరెంట్‌ను గమనించారు.^[3] ఆయన విద్యుత్తు లీడ్స్ కల ఒక బార్ అయస్కాంతం వద్ద ఒక రాగి డిస్క్ భ్రమణ ద్వారా స్థిరమైన కరెంట్‌ను ఉత్పత్తి చేశారు. (ఫారడేస్ డిస్క్).^[8]. అతను శక్తి యొక్క రేఖలు అనే ప్రత్యయం ఉపయోగించి విద్యుదయస్కాంత ప్రేరణ వివరించారు. కానీ శాస్త్ర వేత్తలు కేవలం వాటిని గణిత౦లో రూపొందించనందున అతని సైద్ధాంతిక ఆలోచనలను విస్తృతంగా తిరస్కరించారు. కానీ మక్స్వేల్ మాత్రం తన పరిమాణ విద్యుతయస్కాంత సిద్ధాంతమును ఫారడే ఆలోచనల మూల ఆధారంగా చేశారు. మాక్స్వెల్ యొక్క పత్రాలలో, సమయంతో మారే విద్యుదయస్కాంత ప్రేరణను ఒక అవకలన సమీకరణంగా వ్యక్తపరిచారు. అది మోషనల్ ఈఎమ్‌ఎఫ్‌ను వివరించకపోయినా ఇంకా రూపంలో ఫారాడే అసలైన చట్టము కాకపోయిన ఓలివర్ హీవిసైడ్ ఫారడే నియమం గానే పిలిచారు. ప్రస్తుతం హీవిసైడ్ కథన౦ యొక్క రూపమే మాక్స్వెల్ సమీకరణములలో గుర్తించబడుతుంది. హీంరిచ్ లెంజ్ 1834 సం.లో లెంజ్ సూత్రమును సూత్రీకరించారు. అది సర్క్యూట్ లోని ధారను వివరిస్తుంది. అలాగే ప్రేరిత ఈఎమ్‌ఎఫ్‌ను, విద్యుదయస్కాంత ప్రేరణ ఫలితంగా వచ్చే కరెంట్ యొక్క దిశలను కూడా ఇస్తుంది.

ఫారడే సూత్రం

గుణాత్మక ప్రకటన

ఒక క్లోజ్డ్ సర్క్యూట్ లో ప్రేరేపించబడిన ఎలక్ట్రోమోటివ్ ఫోర్స్ ఆ సర్క్యూట్ ద్వారా ఉన్నఅయస్కాంత ధార యొక్క సమయంతో మారే రేటు యొక్క ప్రతికూల సమానం. ఫెరడే సూత్రం యొక్క ఈ వెర్షన్ కచ్చితంగా క్లోజ్డ్ సర్క్యూట్ అనంతమైన సన్నని తీగ యొక్క లూప్ అయినప్పుడు మాత్రమే చెల్లును, క్రింద చర్చించిన ఇతర పరిస్థితులలో చెల్లదు. మరొక రూపం, మాక్స్వెల్-ఫెరడే సమీకరణం (దిగువ పేర్కొన్న), అన్ని పరిస్థితులలో చెల్లుతుంది.

పరిమాణాత్మక ప్రకటన

ఫారడే ప్రేరణ నియమం ఒక ఊహాత్మక ఉపరితల (దేని సరిహద్దు ఒక వీర్యమో) Σ ద్వారా అయస్కాంత ఫ్లక్స్ Φ_Bను వినియోగించుకుంటుంది. వీర్యంతో సమయంతో కదులుతూ ఉండవచ్చు అందువలన ఉపరితల కోసం Σ (t) వ్రాయాలి. అయస్కాంత ధార సమగ్ర ఉపరితల నిర్వచించబడింది:

\Phi _{\mathrm {B} }=\iint \limits _{\Sigma (t)}\mathbf {B} (\mathbf {r} ,t)\cdot d\mathbf {A} \,

dA అనగా కదిలే ఉపరితల Σ(t) యొక్క ఉపరితల ప్రాంత౦ యొక్క ఒక మూలకం. B అనగా అయస్కాంత రంగం, B·dA అనగా డాట్ గుణకం వైర్ లూప్ ద్వారా అయస్కాంత ఫ్లక్స్ ఆ లూప్ గుండా వెలుతున్న అయస్కాంత ఫ్లక్స్ రేఖల సంఖ్య నిష్పత్తిలో ఉంటుంది.అయస్కాంత ధార B మారడం వల్ల, ఆ వీర్యం కదలడం వల్ల లేదా ఆ వీర్యం యోక్క రూపం మారడం వల్ల మారచ్చు. అప్పుడు ఆ వీర్యానికి EMF ${\mathcal {E}}$ లభిస్తుంది. ${\mathcal {E}}$ ను వైర్ లూప్ చుట్టూ ఒకసారి ప్రయాణించిన ఆ యూనిట్ విద్యుదావేశం అందుబాటులో ఉన్న శక్తిగా నిర్వచించారు. సరిసమానంగా ఇది వైర్ ను కత్తరించి సృష్టించిన బహిరంగ సర్క్యూట్ కు లీడ్స్ అతికించి వోల్టామీటర్ కొలవబడుతుంది. లోరెంట్జ్-శక్తి సూత్రం ప్రకారం (ఎస్.ఐ యూనిట్లలో) :

\mathbf {F} =q\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)

ఒక వైర్ లూప్ లో ఉన్న ఈ‌ఎం‌ఎఫ్:

{\mathcal {E}}={\frac {1}{q}}\oint _{\mathrm {wire} }\mathbf {F} \cdot d{\boldsymbol {\ell }}=\oint _{\mathrm {wire} }\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)\cdot d{\boldsymbol {\ell }}

E అనగా విద్యుత్ రంగం, B అనగా అయస్కాంత రంగం (అయస్కాంత ఫ్లక్స్ సాంద్రత, అయస్కాంత ప్రేరణ), dℓ అనగా వైర్ పాటు ఒక అణుమాత్రమైన ఆర్క్ పొడవు. EMF అయస్కాంత ధార యొక్క మార్పు రేటు ద్వారా ఇవ్వబడుతుంది:

{\mathcal {E}}=-{{d\Phi _{B}} \over dt}\

${\mathcal {E}}$ అనగా వోల్ట్లలో ఎలక్ట్రోమోటివ్ ఫోర్స్ (EMF) , Φ_B అనగా వెబెర్లలో ఉన్న అయస్కాంత ధార.ఎలక్ట్రోమోటివ్ ఫోర్స్ యొక్క దిశ లేన్జ్ లా ద్వారా ఇవ్వబడుతుంది. ఒక గెట్టిగా చుట్టబడిన తీగ యొక్క కాయిల్ (N ఒకేలా ఉన్న మలుపులు ఉన్నాయి, ప్రతి మలుపుకు ఒకటే Φ_B ఉంది) కు ఫారడే ప్రేరణ నియమం ఇలా మారుతుంది.

{\mathcal {E}}=-N{{d\Phi _{B}} \over dt}

N తీగ మలుపుల యొక్క సంఖ్య, Φ_B ఒక లూప్ ద్వారా వెబర్లలో ఉన్న అయస్కాంత ధార.

మాక్స్వెల్-ఫెరడే సమీకరణం

మాక్స్వెల్-ఫెరడే సమీకరణం ఫారడే ప్రేరణ నియమం యొక్క సాధారణీకరణ.దీని ప్రకారం సమయంతో మారే అయస్కాంత రంగం ఎల్లప్పుడూ ఒక ప్రాదేశికంగా మారే, సాంప్రదాయిక విద్యుత్ రంగంతో కలిసి వస్తుంది

$\nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}$ (యెస్.ఐ యూనిట్లలో)

$\nabla \times$ అనగా కర్ల్ ఆపరేటర్, మళ్లీ E (r, t) అనగా విద్యుత్ రంగం, B (r, t) అనగా అయస్కాంత రంగం. ఈ రంగాలు సాధారణంగా స్థానం r, సమయం t యొక్క విధులుగా ఉంటాయి. మాక్స్వెల్-ఫెరడే సమీకరణం నాలుగు మాక్స్వెల్ సమీకరణాలలో ఒకటి, అందువలన క్లాసికల్ ఎలెక్త్రోమాగ్నెటిసం సిద్ధాంతంలో ప్రాథమిక పాత్ర పోషిస్తుంది. ఇది కెల్విన్ స్టోక్స్ సిద్ధాంతం ద్వారా ఒక అంతర్గత రూపంలో వ్రాయవచ్చు.

$\oint _{\partial \Sigma }\mathbf {E} \cdot d{\boldsymbol {\ell }}=-\int _{\Sigma }{\frac {\partial \mathbf {B} }{\partial t}}\cdot d\mathbf {A}$

Σఅనగా మూసివున్న ఆకృతి ∂Σ హద్దుగా ఉపరితల. E అనగా విద్యుత్ రంగం, B అనగా అయస్కాంత రంగం. dℓఅనగా ఆకృతి ∂Σ యొక్క ఒక అణుమాత్రమైన వెక్టర్ అంశం. dA అనగా ఉపరితలం Σ యొక్క ఒక అణుమాత్రమైన వెక్టర్ అంశం.ఒక వేల దాని దిశ ఉపరితల సవరిత భాగానికి లంబకోనియంగా ఉంటే పరిమాణం ఉపరితలం మీద ఉన్న ఒక అణుమాత్రమైన సవరిత భాగ౦ యొక్క పరిధి అవును. dℓ, dA యొక్క సంజ్ఞలో సందిగ్ధత ఉంటుంది. కుడి చేయి నియమం వాడి సరియైన సంజ్ఞను తెలుసుకోవచ్చు. ఒక సమతల ఉపరితలం Σ కు, రేఖ ∂Σ యొక్క సానుకూల మార్గమూలకం dℓ అనేది కుడి చేయి నియమం చేత ఎప్పుడైతే చూపుడు వేలు ఉపరితల నార్మల్ n దిశలో ఉంటుందో అప్పుడు ఏ దిశలో ఐతే కుడి చేయి వేళ్లు ఉంటాయో ఆ దిశగా నిర్వచించబడింది. ∂Σ చుట్టూ చలమును మార్గ చలము లేదా లైన్ చలము అంటారు. మార్గ చలము యొక్క సున్నా కానీ ప్రవర్తన అచలమైన విద్యుధావేశాల నుండి ప్రతిఫలించే రంగంయొక్క ప్రవర్తనకు భిన్నంగా ఉంది. ఈ చలము సమీకరణం ప్రదేశం లోని ఏ మార్గం ∂Σ కైనా, ఏ ఉపరితలం Σ కైనా దేని సరిహద్దు ఐతే ఆ మార్గమో దానికి పరివర్తిస్తుంది. మార్గం Σ సమయంలో మారకపోతే ఆ సమీకరణాన్ని మరల ఇలా రాయొచ్చు.

\oint _{\partial \Sigma }\mathbf {E} \cdot d{\boldsymbol {\ell }}=-{\frac {d}{dt}}\int _{\Sigma }\mathbf {B} \cdot d\mathbf {A} .

కుడి వైపు ఉన్న ఉపరితల చలము Σ ద్వారా అయస్కాంత ఫ్లక్స్ ΦB యొక్క స్పష్టమైన వ్యక్తీకరణ.

ఫారడే సూత్రానికి రుజువు

నాలుగు మాక్స్వెల్ సమీకరణాలు, లారెంజ్ శక్తి నియమంతో పాటు, క్లాసికల్ ఎలెక్ట్రోమాగ్నెటిసమ్ లో ప్రతిదీ ఉత్పాదించడానికి తగిన పునాది అవుతాయి. ఒక కదిలే లూప్ (వైశాల్యము $\Sigma (t)$ :) ద్వారా ఉన్న ధర యొక్క సమయ డెరివేటివ్ ను పరిగణించండి.

{\frac {d\Phi _{B}}{dt}}={\frac {d}{dt}}\int _{\Sigma (t)}\mathbf {B} (t)\cdot d\mathbf {A}

చలము రెండు కారణాల కాలక్రమేణా మారవచ్చు: అనుకలము మారవచ్చు, లేదా అనూకలన ప్రాంతం మారవచ్చు. ఈ అందువలన, ఏకగణంగా జోడించవచ్చు

\left.{\frac {d\Phi _{B}}{dt}}\right|_{t=t_{0}}=\left(\int _{\Sigma (t_{0})}\left.{\frac {\partial \mathbf {B} }{\partial t}}\right|_{t=t_{0}}\cdot d\mathbf {A} \right)+\left({\frac {d}{dt}}\int _{\Sigma (t)}\mathbf {B} (t_{0})\cdot d\mathbf {A} \right)

't₀అనేది ఒక తెలిసిన మారని సమయం. కుడి వైపు ఉన్న మొదటి భాగం ట్రాన్స్ఫోర్మర్ emf కు, రెండవ భాగం మోషనల్ emf కు సంబంధించినవి అని చూపిస్తాము. కుడి వైపు ఉన్న మొదటి భాగాన్ని మాక్స్వెల్-ఫెరడే సమీకరణ యొక్క అనుకలన రూపం వాడి ఇలా వ్రాయొచ్చు:

\int _{\Sigma (t_{0})}\left.{\frac {\partial \mathbf {B} }{\partial t}}\right|_{t=t_{0}}\cdot d\mathbf {A} =-\oint _{\partial \Sigma (t_{0})}\mathbf {E} (t_{0})\cdot d{\boldsymbol {\ell }}

తరువాత, కుడి వైపు రెండవ భాగమును విశ్లేషిద్దాము

{\frac {d}{dt}}\int _{\Sigma (t)}\mathbf {B} (t_{0})\cdot d\mathbf {A}

ఇది రుజువు యొక్క అత్యన్త కష్టమైన భాగం.ఆ లూప్ కదిలినా లేదా లూప్ యొక్క ఆకారం మారినా అది ఒక ఉపరితలమును తుడుస్తుంది.ఈ తుడిచిన ఉపరితలం ద్వారా ఉన్న అయస్కాంత ధార ఆ లూప్ లోనికి వచ్చే లేదా నిష్క్రమించే అయస్కాంత ధారకు సంబంధించింది.అందువలన ఈ అయస్కాంత ధార నే సమయ డెరివేటివ్ కు కారణం అవుతుంది.ఇక్కడ గాస్ తొక్క అయస్కాంత సూత్రమును గర్భితముగా వాడుతున్నాము.ఎందుకంటే ఫ్లక్స్ పంక్తులకు ఆది కానీ అంతము కానీ ఉండవు.అవి కేవలం లూప్ లోనికి రాగలవు. ఆ లూప్ యొక్క చిన్న భాగం $d{\boldsymbol {\ell }}$ వేగం v తో సమయం $dt$ కదిలితే అది ఒక వెక్టర్ విస్తీర్ణం $d\mathbf {A} =\mathbf {v} \,dt\times d{\boldsymbol {\ell }}$ ను తుడుస్తుంది.అందువలన ఇక్కడ అయస్కాంత ధార లోని మార్పు : $\mathbf {B} \cdot (\mathbf {v} \,dt\times d{\boldsymbol {\ell }})=-dt\,d{\boldsymbol {\ell }}\cdot (\mathbf {v} \times \mathbf {B} )$ అందువలన

{\frac {d}{dt}}\int _{\Sigma (t)}\mathbf {B} (t_{0})\cdot d\mathbf {A} =-\oint _{\partial \Sigma (t_{0})}(\mathbf {v} (t_{0})\times \mathbf {B} (t_{0}))\cdot d{\boldsymbol {\ell }}

v అనగా ఆ లూప్ $\partial \Sigma$ మీద ఉన్న ఒక బిందువు యొక్క వేగం

\left.{\frac {d\Phi _{B}}{dt}}\right|_{t=t_{0}}=\left(-\oint _{\partial \Sigma (t_{0})}\mathbf {E} (t_{0})\cdot d{\boldsymbol {\ell }}\right)+\left(-\oint _{\partial \Sigma (t_{0})}(\mathbf {v} (t_{0})\times \mathbf {B} (t_{0}))\cdot d{\boldsymbol {\ell }}\right)

EMF ను వీర్యం చుట్టూ ఒకసారి ప్రయాణించిన ఆ యూనిట్ విద్యుదావేశానికి అందుబాటులో ఉన్న శక్తిగా నిర్వచించారు.లోరెంట్జ్ శక్తి నియమం ప్రకారం : $EMF=\oint \left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)\cdot {\text{d}}{\boldsymbol {\ell }}$

ఈ రెండింటినీ కలిపితే ${\frac {d\Phi _{B}}{dt}}=-EMF$

ఫారడే నియమానికి వ్యతిరేక ఉదాహరణలు

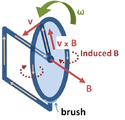
ఫెరడే డిస్క్ విద్యుత్ ఉత్పాదక. డిస్క్ స్టాటిక్ అయస్కాంత రంగం B లో కోణీయ వేగ ω తో తిరుగుతూ వృత్తాకారంలో ఆ వాహక వ్యాసార్థమును తుడుస్తుంది. అయస్కాంత లారెంజ్ బలము v × B ఆ వాహక వ్యాసార్థం గుండా కరెంట్ ను వాహక చట్రం వరకు నడిపిస్తుంది, ఇక్కడి నుండి కింద ఉన్న బ్రష్, డిస్క్ కు సహాయంగా ఉన్న ఇరుసు ద్వారా సర్క్యూట్ పూర్తి అవుతుంది. "సర్క్యూట్" ఆకారంలో స్థిరంగా ఉంది, సర్క్యూట్ ద్వారా ఫ్లక్స్ కాలముతో మారదు అయినా ఈ పరికరం, EMF ను, కరెంట్ ను ఉత్పత్తి చేస్తుంది.
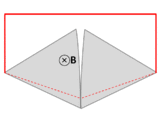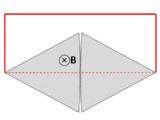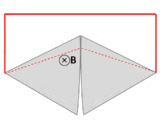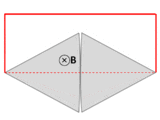
ఒక వైర్ (ఘనమైన ఎరుపు పంక్తులు) ఒక సర్క్యూట్ ఏర్పాటు చేయడానికి రెండు తగులుకుంటున్న లోహ ప్లేట్లు (వెండి) ను కలుపుతుంది. మొత్తం వ్యవస్థ పేజీకు లంబకోనియంగా ఒకే అయస్కాంత రంగంలో, కూర్చుంటుంది. ఒక వేల "సర్క్యూట్" అనే పదాన్ని (ఎర్ర మార్క్) "కరెంట్ ప్రవాహం యొక్క ప్రాధమిక మార్గం"గా వ్యాక్యాణిస్తే, అప్పుడు ప్లేట్లు తిరిగినప్పుడు"సర్క్యూట్" గుండా ప్రవహించే అయస్కాంత ధార చాలా బాగా మారినప్పిటికి EMF మాత్రం ఫెరడే సూత్రానికి విరుద్ధంగా దాదాపు సున్నా నే ఉంటుంది.

హోమోపోలర్ జెనరేటర్ ఒక ఉదాహరణ. సజాతీయమైన అయస్కాంత రంగంలో తిరుగున్న వృత్తాకార లోహ డిస్క్ ఒక DC (సమయంలో స్థిరమైన) EMF ఉత్పత్తి చేస్తుంది. ఫెరడే సూత్రం ప్రకారం, EMF అయస్కాంత ధార యొక్క సమయ డెరివేటివ్, అందువలన ఒక DC EMF అనేది నిరంతరం పెరుగుతూ ఉన్న అయస్కాంత ధార వల్ల మాత్రమే సాధ్యమవుతుంది. కానీ జెనరేటర్ లో, అయస్కాంత రంగం స్థిరంగా ఉంది, డిస్క్ అదే స్థానంలో ఉంది, అందువలన అయస్కాంత ధార నిరంతరం పెరగటం లేదు. కాబట్టి ఈ ఉదాహరణ ఫెరడే సూత్రంతో నేరుగా విశ్లేషించలేము. ఫెయ్న్మన్ ఇచ్చిన మరొక ఉదాహరణలో emf తక్కువగా ఉన్నప్పటికీ సర్క్యూట్ గుండా ఉన్న అయస్కాంత ధార చాలా బాగా మారుతుంది. అధికసంఖ్యాకంలో పరిక్షేపము వలన, వర్క్ ఫంక్షన్ నిర్భందం వలన ఒక వస్తువులోని ఎలక్ట్రాన్లు ఆ వస్తువులో ఉండే అణువులను అనుసరించడానికి ప్రయత్నిస్తాయి.ఎప్పుడైతే వస్తువు లోని అణువులు వాటి ఎలక్ట్రాన్లను లాగుతూ కదులుతుంటాయో, ఎలక్ట్రాన్ల మీద లోరెంట్జ్ శక్తి పనిచేసి మోషనల్ emf ఉత్పత్తి అవుతుంది.హోమోపోలర్ జెనరేటోర్ లో సర్క్యూట్ యొక్క జ్యామితి అలాగే ఉన్నప్పటికి వస్తువు యొక్క అణువులు కదులుతున్నాయి. రెండవ ఉదాహరణలో జ్యామితి చాలా ఎక్కువగా మారుతున్నప్పటికి అణువులు అచలంగా ఉన్నాయి. ఫారడే నియమం సన్నటి వైర్లకు ఎల్లప్పుడూ వర్తిస్తుంది, ఎందుకంటే అక్కడ సర్క్యూట్ యొక్క జ్యామితి అణువులు ఎలా కదిలితే అలాగే మరుతుంది . ఫెరడే సూత్రం అన్ని పరిస్థితులకు వర్తించనప్పటికీ, మాక్స్వెల్-ఫెరడే సమీకరణం, లోరెంజ్ ఫోర్స్ నియమం ఎల్లప్పుడూ సరైనవి, ఎల్లప్పుడూ నేరుగా ఉపయోగించవచ్చు.పై రెండు ఉదాహరణలలో సరియైన అనుకలన మార్గము ఎంచుకొని పని చేస్తే సరైన ఫలితాలు వస్తాయి.సన్నటి వైర్లు కానప్పుడు అనుకలన మార్గం అతి చిన్నదైన నేరు మార్గంలో వాహకం గుండా తీసుకోకూడదు. (ఇది ఎఫ్.హుఘ్స్, ఎఫ్.జె.యంగ్, జాన్ విలే వ్రాసిన "ద్రవం యొక్క విద్యుదయస్కాంత డైనమిక్స్"లో వివరంగా వివరించబడింది).

ప్రయోగములు

విద్యుదయస్కాంత ప్రేరణ సూత్రాలను అనేక పరికరాలు, వ్యవస్థలలో ఉపయోగాలు ఉన్నాయి ఉదాహరణగా : కరెంట్ క్లాంప్, విద్యుత్ ఉత్పత్తులు, ఎలెక్ట్రోమాగ్నెటిక్ ఫోర్మింగ్, గ్రాఫిక్స్ టాబ్లెట్, హాల్ ఎఫెక్ట్ మీటర్లు, ఇండక్షన్ మోటర్లు, ఇండక్షన్ కుక్కర్లు, ఇండక్షన్ సీలింగ్, ఇండక్షన్ వెల్డింగ్, ఇండక్షన్ ఛార్జింగ్, ఇండక్టర్లు, అయస్కాంత ఫ్లో మీటర్లు, పిక్కప్స్, రోలాండ్ రింగు, ట్రాన్స్క్రేనియల్ మాగ్నెటిక్ స్టిములేషన్, ట్రాన్స్ఫోర్మలు, వైర్లు లేని శక్తి మార్పిడి ఇంకా ఎన్నో.

మూలాలు

↑ Sadiku, M. N. O. (2007). Elements of Electromagnetics (fourth ed.). New York (USA)/Oxford (UK): Oxford University Press. p. 386. ISBN 0-19-530048-3.
↑ "Applications of electromagnetic induction". Boston University. 1999-07-22.
↑ ^3.0 ^3.1 Giancoli, Douglas C. (1998). Physics: Principles with Applications (Fifth ed.). pp. 623–624.
↑ Faraday, Michael; Day, P. (1999-02-01). The philosopher's tree: a selection of Michael Faraday's writings. CRC Press. p. 71. ISBN 978-0-7503-0570-9. Retrieved 28 August 2011.
↑ Ulaby, Fawwaz (2007). Fundamentals of applied electromagnetics (5th ed.). Pearson:Prentice Hall. p. 255. ISBN 0-13-241326-4.
↑ "Joseph Henry". Distinguished Members Gallery, National Academy of Sciences. Archived from the original on 2006-12-09. Retrieved 2006-11-30.
↑ Michael Faraday, by L. Pearce Williams, p. 182-3
↑ Michael Faraday, by L. Pearce Williams, p. 191–5

ఇతర లింకులు

[Sadiku386-1] Sadiku, M. N. O. (2007). Elements of Electromagnetics (fourth ed.). New York (USA)/Oxford (UK): Oxford University Press. p. 386. ISBN 0-19-530048-3.

[2] "Applications of electromagnetic induction". Boston University. 1999-07-22.

[Giancoli-3] 3.0 ^3.1 Giancoli, Douglas C. (1998). Physics: Principles with Applications (Fifth ed.). pp. 623–624.

[FaradayDay1999-4] Faraday, Michael; Day, P. (1999-02-01). The philosopher's tree: a selection of Michael Faraday's writings. CRC Press. p. 71. ISBN 978-0-7503-0570-9. Retrieved 28 August 2011.

[5] Ulaby, Fawwaz (2007). Fundamentals of applied electromagnetics (5th ed.). Pearson:Prentice Hall. p. 255. ISBN 0-13-241326-4.

[6] "Joseph Henry". Distinguished Members Gallery, National Academy of Sciences. Archived from the original on 2006-12-09. Retrieved 2006-11-30.

[7] Michael Faraday, by L. Pearce Williams, p. 182-3

[8] Michael Faraday, by L. Pearce Williams, p. 191–5

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]