వృత్త చాపం

వృత్తాకార సెక్టర్ ఆకుపచ్చ రంగులో ఉంటుంది. పొడవు L దాని వక్రం సరిహద్దు ఒక వృత్తాకార చాపం.

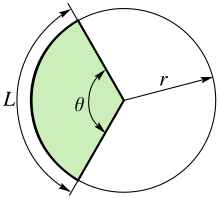
వృత్తాకార చాపం అనేది ఒక జత విభిన్న బిందువుల మధ్య ఉన్న వృత్త భాగం . రెండు బిందువులు ఒకదానికొకటి నేరుగా ఎదురుగా లేకుంటే, ఈ చాపాలలో ఒకటి, లఘు చాపం, వృత్తం మధ్యలో π రేడియన్‌ల (180 డిగ్రీలు) కంటే తక్కువ కోణాన్ని కలిగి ఉంటుంది ; ఇతర ఆర్క్, గురు చాపం, π రేడియన్‌ల కంటే ఎక్కువ కోణాన్ని కలిగి ఉంటుంది. వృత్తం యొక్క చాపం ఒక వృత్తం యొక్క చుట్టుకొలత యొక్క భాగం లేదా విభాగంగా నిర్వచించబడింది. చాపం యొక్క రెండు చివరలను కలిపే సరళ రేఖను వృత్తం యొక్క జ్యా అంటారు. చాపం యొక్క పొడవు సరిగ్గా వృత్తంలో సగం ఉంటే, దానిని అర్ధ వృత్తాకార చాపం అంటారు.

పొడవు

r వ్యాసార్థం కలిగి యున్న వృత్త చాపం కేంద్రంతో θ (రేడియన్‌లలో కొలుస్తారు) కోణాన్ని చేస్తే దాని చాపం పొడవు:

$L=\theta r.$

దీనికి కారణం

${\frac {L}{\mathrm {circumference} }}={\frac {\theta }{2\pi }}.$

చుట్టుకొలత సూత్రాన్ని ప్రతిక్షేపిస్తే

${\frac {L}{2\pi r}}={\frac {\theta }{2\pi }},$

,, α ఒకే కోణంలో డిగ్రీలలో కొలుస్తారు, θ = α/180π,, ఆర్క్ పొడవు సమానం

$L={\frac {\alpha \pi r}{180}}.$

వృత్తంలో చాపం యొక్క పొడవును నిర్ణయించడానికి ఒక ఆచరణాత్మక మార్గం ఏమిటంటే, చాపం యొక్క ముగింపు బిందువుల నుండి వృత్తం కేంద్రానికి రెండు వ్యాసార్థాలు గీయడం, వాటి మధ్య కోణాన్ని కొలవడం, ఆపై కింది సూత్రాన్ని ఉపయోగించి చాపం పొడవును కనుగొనడం.

డిగ్రీలు/360° = L / చుట్టుకొలతలో కోణం యొక్క కొలత.

ఉదాహరణకు, కోణం యొక్క కొలత 60 డిగ్రీలు, చుట్టుకొలత 24 అంగుళాలు అయితే, అప్పుడు

${\begin{aligned}{\frac {60}{360}}&={\frac {L}{24}}\\[6pt]360L&=1440\\[6pt]L&=4.\end{aligned}}$

వృత్తం యొక్క చుట్టుకొలత, వృత్తం యొక్క డిగ్రీలు, ఎల్లప్పుడూ 360 ఉండేవి, ఇది నేరుగా అనుపాతంలో ఉంటుంది.

వృత్తం యొక్క ఎగువ సగం ఇలా పారామితి చేయవచ్చు

$y={\sqrt {r^{2}-x^{2}}}.$

అప్పుడు నుండి చాపం పొడవు $x=a$కు $x=b$ ఉంది

$L=r{\Big [}\arcsin \left({\frac {x}{r}}\right){\Big ]}_{a}^{b}.$

సెక్టార్ ప్రాంతం

ఒక చాపం, వృత్తం మధ్యలో ఏర్పడిన సెక్టార్ వైశాల్యం (చాపం, దాని ముగింపు బిందువులకు గీసిన రెండు వ్యాసార్థాలతో సరిహద్దులు)

$A={\frac {r^{2}\theta }{2}}.$

A ప్రాంతం వృత్త వైశాల్యానికి θ కోణంతో పూర్తి వృత్తానికి సమానమైన నిష్పత్తిని కలిగి ఉంటుంది:

${\frac {A}{\pi r^{2}}}={\frac {\theta }{2\pi }}.$

మనం రెండు వైపులా π రద్దు చేయవచ్చు:

${\frac {A}{r^{2}}}={\frac {\theta }{2}}.$

రెండు వైపులా r ² చే గుణించడం ద్వారా, మనం తుది ఫలితాన్ని పొందుతాము:

$A={\frac {1}{2}}r^{2}\theta .$

పైన వివరించిన మార్పిడిని ఉపయోగించి, డిగ్రీలలో కొలవబడిన కేంద్ర కోణం కోసం సెక్టార్ యొక్క వైశాల్యం

$A={\frac {\alpha }{360}}\pi r^{2}.$

వృత్త ఖండం ప్రాంతం

చాపం, దాని రెండు చివరి బిందువుల మధ్య సరళ రేఖతో సరిహద్దులుగా ఉన్న ఆకారం యొక్క వైశాల్యం

${\frac {1}{2}}r^{2}(\theta -\sin \theta ).$

వృత్త ఖండం యొక్క వైశాల్యాన్ని పొందడానికి, మనం వృత్త కేంద్రం, చాపం పొడవు యొక్క రెండు చివరి బిందువులచే నిర్ణయించబడిన త్రిభుజం యొక్క వైశాల్యాన్ని సెక్టరు ప్రాంతం నుండి తీసివేయాలి. $A$ . వివరాల కోసం వృత్తాకార విభాగాన్ని చూడండి.

వ్యాసార్థం

AP, PB అనే రేఖాఖండాల లబ్ధం CP, PD అనే రేఖాఖండాల లబ్ధానికి సమానం . చాపం వెడల్పు AB ఎత్తు CP కలిగి ఉంటే, అప్పుడు వృత్తం యొక్క వ్యాసం $CD={\frac {AP\cdot PB}{CP}}+CP$

జ్యా ఖండన సిద్ధాంతాన్ని ఉపయోగించి ఒక వృత్తం యొక్క వ్యాసార్థం r ఎత్తు H, ఒక చాపం వెడల్పు W ఇవ్వబడుతుంది:

చాపం వలె అదే చివరి బిందువులతో జ్యాను పరిగణించండి. దాని లంబంగా ఉన్న సమద్విఖండన చేసిన మరో జ్యా, ఇది వృత్తం యొక్క వ్యాసం. మొదటి జ్యా యొక్క పొడవు W, ఇది రెండు సమాన భాగాలుగా విభజించబడింది, ఒక్కొక్కటి పొడవుతో W/2 . వ్యాసం యొక్క మొత్తం పొడవు 2 r, ఇది మొదటి జ్యా ద్వారా రెండు భాగాలుగా విభజించబడింది. ఒక భాగం యొక్క పొడవు చాపం యొక్క సాగిట్టా, H, మరొక భాగం వ్యాసం యొక్క మిగిలిన భాగం, పొడవు 2 r - H . ఈ రెండు జ్యాలకు ఖండన తీగ సిద్ధాంతాన్ని వర్తింపజేయడం ఉత్పత్తి అవుతుంది

$H(2r-H)=\left({\frac {W}{2}}\right)^{2},$

$2r-H={\frac {W^{2}}{4H}},$

కాబట్టి

$r={\frac {W^{2}}{8H}}+{\frac {H}{2}}.$

బాహ్య లంకెలు

• గణితం ఓపెన్ రిఫరెన్స్ సర్కిల్ పేజీల కోసం విషయాల పట్టిక
• ఇంటరాక్టివ్ యానిమేషన్‌తో వృత్తాకార ఆర్క్‌లపై గణితం ఓపెన్ రిఫరెన్స్ పేజీ
• ఇంటరాక్టివ్ యానిమేషన్‌తో వృత్తాకార ఆర్క్ లేదా సెగ్మెంట్ యొక్క వ్యాసార్థంపై గణితం ఓపెన్ రిఫరెన్స్ పేజీ