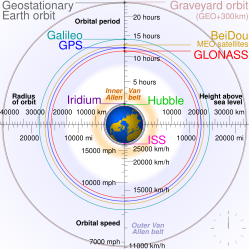
భూ స్థిర కక్ష్య
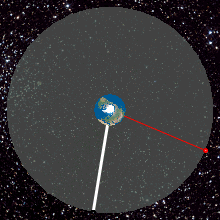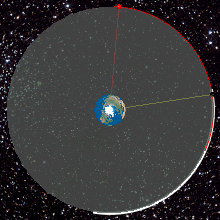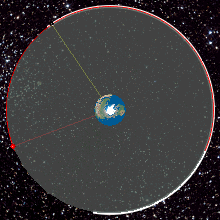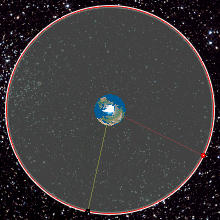
భూమధ్య రేఖపై 35,786 కి.మీ ఎత్తులో భూభ్రమణ దిశలో, భూమధ్య రేఖాతలానికి సున్నా డిగ్రీల కోణంలో ఉండే వృత్తాకార కక్ష్యను భూ స్థిర కక్ష్య అంటారు. దీన్ని ఇంగ్లీషులో జియోస్టేషనరీ ఆర్బిట్ అంటారు. అటువంటి కక్ష్యలోని ఏ వస్తువైనా భూ భ్రమణ వేగంతో సమానమైన వేగంతో భూమి చూట్టూ తిరగడం వలన, భూమిపై ఉన్న పరిశీలకులకు కదలకుండా, స్థిరంగా, ఉన్నచోటే ఉన్నట్లు కనిపిస్తుంది. సమాచార ఉపగ్రహాలు, వాతావరణ ఉపగ్రహాలు, అప్పుడప్పుడు ఈ కక్ష్యలో ప్రక్షేపిస్తారు. తద్వారా నేలమీద, ఉపగ్రహ స్థానాన్ని బట్టి ఏంటెన్నా దిశలు మార్చవలసిన అవసరం తప్పుతుంది.
సమాచార వ్యవస్థలకోసమై "భూస్థిరకక్ష్య" అనే పరిభావన, హెర్మన్ పొటోన్మిక్ 1928లో ప్రచురించిన ఒక పరిశోధనా పత్రంలో చూచాయగా పేర్కొనబడింది.[1] ప్రసిద్ధ రచనల్లో భూస్థిర కక్ష్య అనే భావన జార్జ్. ఓ. స్మిత్ రాసిన మొదటి 'వీనస్ ఎక్విలేటరల్' (Venus Equilateral s)అనే కథలో కనబడింది, అయితే, జార్జ్. ఓ. స్మిత్ దీనికి అంతగా ప్రాధన్యత ఇవ్వలేదు.[2] 1945లో ప్రసిద్ధ వైజ్ఞానిక కాల్పనిక రచయిత ఆర్థర్ సి. క్లార్క్, వైర్ లెస్ వరల్డ్ పత్రికలో ప్రచురించిన "Extra-Terrestrial Relays — Can Rocket Stations Give Worldwide Radio Coverage?" (గ్రహాంతర ప్రసారాలు - అంతరిక్ష స్థావరాలు ప్రపంచవ్యాప్తంగా రేడియో కవరేజిని ఇవ్వగలవా?)అనే పరిశోధనా పత్రంలో విపులంగా చర్చించాడు.[3] ప్రసార ఉపగ్రహాలకి ఉపయోగపడే కక్ష్య[4] గా, క్లార్క్ చేత విపులంగా చర్చించబడిన కారణంగా, దీనిని క్లార్క్ కక్ష్య (Clarke Orbit)గా కూడా పిలుస్తారు.[5] భూమధ్యరేఖపైన సముద్రతలానికి 35,786 కి.మీ ఎత్తున ఉన్న ప్రాంతాన్ని క్లార్క్ వలయం (Clarke Belt)గా పేర్కొంటారు.
ఆచరణలో ఉపయోగాలు
[మార్చు]సమాచార ఉపగ్రహాలు, ప్రసార ఉపగ్రహాలు, SBAS (Satellite-based augmentation system - ఉపగ్రహ ఆధారిత అభివృద్ధి వ్యవస్థ) ఉపగ్రహాలలో పెక్కుశాతం భూస్థిరకక్ష్యలోనే పరిభ్రమిస్తూ ఉంటాయి. భూ లఘు కక్ష్యలోని వస్తువుని భూ స్థిరకక్ష్యలోనికి భూస్థిర బదలాయింపు కక్ష్య ద్వారా చేస్తారు (ఉన్నత అక్షాంశాల మధ్యనున్న ప్రేక్షకులున్న కారణాన, రష్యా దూరదర్శన ఉపగ్రహాలు అండాకార మొల్నియా, టుండ్రా కక్ష్యలను ఉపయోగించుకునేవి). 1964 లో డెల్టా - డి రాకెట్ సింకోమ్ - 3 అనే ఉపగ్రహాన్ని మొట్టమొదటిసారిగా భూస్థిరకక్ష్యలోకి ప్రవేశపెట్టింది.
భూ ఉపరితలం యొక్క దృగ్గోచర, పరారుణ ఛాయాచిత్రాలను పంపించే వాతావరణ ఉపగ్రహాల ప్రపంచవ్యాప్త అల్లిక, భూ స్థిర కక్ష్యలోనే పరిభ్రమిస్తున్నాయి. వీటిల్లో ముఖ్యమైనవి,
- భారతదేశపు INSAT శ్రేణి, ఉపగ్రహాలు
- అమెరికా సంయుక్త రాష్ట్రాల GOES
- ఐరోపా అంతరిక్ష సంస్థ (European Space Agency) చే ప్రయోగింపబడి, ఐరోపా వాతావరణ ఉపగ్రహ సంస్థ (EUMETSAT) చేత నడుపబడుతున్న Meteosat
- జపాన్ దేశపు MTSAT
కక్ష్యా స్థిరత్వం
[మార్చు]సరిగ్గా, భూమధ్యరేఖకు 35,786 కి.మీ (22,236 మైళ్ళు) ఎత్తున మాత్రమే భూ స్థిర కక్ష్య సాధింపబడుతుంది. మరో విధంగా చెప్పాలంటే, 3.07 కి.మీ/సె కక్ష్యా వేగం; లేదా 1,436 నిమిషాల (23.934461223 గంటలు లేదా ఒక రోజు) ఆవర్తన కాలం ఉంటేనే భూ స్థిర కక్ష్య సాధ్యపడుతుంది. అప్పుడు మాత్రమే భూ భ్రమణంతో పోల్చి చూసినపుడు, ఆయా వస్తువులు ఆకాశంలో నిశ్చలంగా కనపిస్తాయి.
చంద్రుని గురుత్వాకర్షణ, సూర్యుని గురుత్వాకర్షణ, తదితర కారాణాల వలన భూస్థిర వస్తువు యొక్క కక్ష్యా తలం, ఆవర్తన చలనం (ఆవర్తన కాలం: 53 సంవత్సరాలు; ప్రారంభ వంపు: 0.85 డిగ్రీలు)లో ఉంటుంది. 0.85 డిగ్రీల ప్రారంభ వంపుగా ప్రారంభమై 26.5 సంవత్సరాలకి 15 డిగ్రీల గరిష్ఠ వంపుకి చేరుతుంది. ఈ ప్రభావాన్ని సరిచేయడానికి, క్రమబద్ధమైన కక్ష్యా స్థిరీకరణ పద్ధతులు అనుసరించాలి. (డెల్టా - వి = ఏడాదికి 50 మి/సె). ఈ పద్ధతిని స్టేషన్ కీపింగ్ అంటారు.
భూమి యొక్క అసౌష్ఠవ రూపం (భూమధ్యరేఖ దీర్ఘవృతాకారంగా ఉండటం) అనేది, రేఖాంశ ఉరవడి అనే ప్రభావాన్ని కలుగజేస్తుంది. ఇందులో రెండు స్థిర సమతుల్యతా స్థానాలు (75.3°తూర్పు వద్ద, 104.7° పడమర వద్ద), రెండు అస్థిర సమతుల్యతా స్థానాలు (165.3°తూర్పు వద్ద, at 14.7° పడమర వద్ద) ఉంటాయి. బయటి నుండి ఏ శక్తి ప్రభావం లేనప్పుడు, భూ స్థిర వస్తువు స్థిర సమతుల్యతా స్థానాల వైపు కదిలిపోతూ ఉంటాయి. తద్వారా వస్తువు యొక్క రేఖాంశ స్థానంలో నిర్ధిష్టమైన మార్పు వస్తూ ఉంటుంది. దీన్ని సరిచేయడానికి గరిష్ఠం డెల్టా - వి 2 మీ/సె (ఏడాదికి) ల కక్ష్యా నియంత్రణ అవసరమౌతుంది (వస్తువు ఉంచవలసిన రేఖాంశాన్ని బట్టి).
సౌర పవనాల, ఉద్గారాల పీడన ప్రభావం కూడా ఉపగ్రహాలు నిర్దేశిత కక్ష్య నుండి పక్కకు పోవడానికి కారణాలౌతూ ఉంటాయి.
భూమి నుండి మరమ్మతు, నిర్వహణ ప్రయోగాలు లేకపోయినా, లేదా ప్రత్యామ్నాయ ఇంధన ఏర్పాట్లు లేకపోయినా, కక్ష్యా స్థిరీకరణ కోసం ఇంధనం వాడబడుతూ ఉండటం వల్ల, వస్తువు యొక్క జీవితకాలం తగ్గిపోతూ ఉంటుంది.
భూస్థిర కక్ష్య ఎత్తు లెక్కింపు
[మార్చు]
భూమ్యాకర్షణ బలం (Fg), ఉపగ్రహం యొక్క కక్ష్యని స్థిరపరిచే అభికేంద్రక బలం (Fc)గా పనిచేస్తుంది. భూస్థిర ఎత్తుని సాధించడాన్ని, ఈ సమీకరణం ద్వారా మొదలుపెట్టాలి.
న్యూటన్ రెండవ చలన నియమం ప్రకారం; ఉపగ్రహంపైన పనిచేస్తున్న బలం F, ఆ ఉపగ్రహం యొక్క ద్రవ్యరాశి m, అ బలం వలన ఉపగ్రహానికి కలిగిన త్వరణము ల లబ్ధానికి సమానం.
పై సమీకరణం లో, రెండువైపులా ఉన్న ఉపగ్రహ ద్రవ్యరాశి m ఉండటాన్ని బట్టి, "భూస్థిర ఎత్తు" ఉపగ్రహ ద్రవ్యరాశి మీద ఆధారపడి ఉండదని తెలుస్తున్నది. అందువల్లన, కక్ష్యావేగానికి అవసరమైన అపకేంద్రక త్వరణం, భూమ్యాకర్షక త్వరణాల పరిమాణాలు సమానమయ్యే స్థానాన్ని గుర్తించడానికి, ఈ సాధన పరిమితమవుతుంది. The centripetal acceleration's magnitude is:
where ω is the angular speed, and r is the orbital radius as measured from the Earth's center of mass.
The magnitude of the gravitational acceleration is:
where M is the mass of Earth, 5.9736 × 1024 kg, and G is the gravitational constant, 6.67428 ± 0.00067 × 10−11 m3 kg−1 s−2.
Equating the two accelerations gives:
![{\displaystyle r^{3}={\frac {GM}{\omega ^{2}}}\to r={\sqrt[{3}]{\frac {GM}{\omega ^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/180afe4e9da7670c6baa5db2fb06811a0469cb02)
The product GM is known with much greater precision than either factor alone; it is known as the geocentric gravitational constant μ = 398,600.4418 ± 0.0008 km3 s−2:
![{\displaystyle r={\sqrt[{3}]{\frac {\mu }{\omega ^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86fc9c7797f74da609ad17740a92d557e33af69e)
The angular speed ω is found by dividing the angle travelled in one revolution (360° = 2π rad) by the orbital period (the time it takes to make one full revolution). In the case of a geostationary orbit, the orbital period is one sidereal day, or 86,164.09054 seconds).[6] This gives:
The resulting orbital radius is 42,164 కిలోమీటర్లు (26,199 మై.). Subtracting the Earth's equatorial radius, 6,378 కిలోమీటర్లు (3,963 మై.), gives the altitude of 35,786 కిలోమీటర్లు (22,236 మై.).
Orbital speed (how fast the satellite is moving through space) is calculated by multiplying the angular speed by the orbital radius:
By the same formula we can find the geostationary-type orbit of an object in relation to Mars (this type of orbit above is referred to as an areostationary orbit if it is above Mars). The geocentric gravitational constant GM (which is μ) for Mars has the value of 42,828 km3s−2, and the known rotational period (T) of Mars is 88,642.66 seconds. Since ω = 2π/T, using the formula above, the value of ω is found to be approx 7.088218×10−5 s−1. Thus, r3 = 8.5243×1012 km3, whose cube root is 20,427 km; subtracting the equatorial radius of Mars (3396.2 km) we have 17,031 km.
ఇవి కూడా చూడండి
[మార్చు]మూలాలు
[మార్చు]- ↑ Noordung, Hermann; et al. (1995) [1929]. The Problem With Space Travel. Translation from original German. DIANE Publishing. p. 72. ISBN 978-0-7881-1849-4.
- ↑ "(Korvus's message is sent) to a small, squat building at the outskirts of Northern Landing. It was hurled at the sky. … It … arrived at the relay station tired and worn, … when it reached a space station only five hundred miles above the city of North Landing." Smith, George O. (1976). The Complete Venus Equilateral. New York: Ballantine Books. pp. 3–4. ISBN 978-0345289537.
- ↑ "It is therefore quite possible that these stories influenced me subconsciously when … I worked out the principles of synchronous communications satellistes …", op. cit, p. x
- ↑ "Extra-Terrestrial Relays — Can Rocket Stations Give Worldwide Radio Coverage?" (PDF). Arthur C. Clark. October 1945. Archived from the original (PDF) on 18 మార్చి 2009. Retrieved 7 ఫిబ్రవరి 2014.
- ↑ "Basics of Space Flight Section 1 Part 5, Geostationary Orbits". NASA. Retrieved 21 June 2009.
- ↑ Edited by P. Kenneth Seidelmann, "Explanatory Supplement to the Astronomical Almanac", University Science Books,1992, pp. 700
ఉల్లేఖన లోపం: "lower-alpha" అనే గ్రూపులో <ref> ట్యాగులు ఉన్నాయి గానీ, దానికి సంబంధించిన <references group="lower-alpha"/> ట్యాగు కనబడలేదు