వృత్తము
| వృత్తము | |
|---|---|

| |
| తలం | ద్విమితీయం |
| నిర్వచనం | ఒకస్థిరబిందువు నుండి సమాన దూరంలోగల బిందుపథం |
| వ్యాసము | కేంద్రంగుండాపోవు జ్యా |
| వ్యాసార్థము | వ్యాసంలో సగభాగం |
| ఆంగ్ల పదం | circle |
| వృత్త పరిధి | వృత్త పరిధి = π(వ్యాసము) |
వృత్తము జ్యామితి అనే గణిత శాస్త్ర విభాగానికి చెందిన ఒక భావన.



ఒక సమతలంలోని ఇవ్వబడిన ఒక బిందువు నుండి సమాన దూరంలో ఉన్న బిందువుల సమితిని వృత్తము అంటారు.అనగా ఒక స్థిర బిందువు నుండి సమాన దూరంలో గల బిందు పథం.ఒక వృత్తం అది ఉండేసమ తలాన్ని మూడు బిందు సమితులుగా విభజిస్తుంది.
- వృత్త బాహ్య బిందువుల సమితి.(వృత్త బాహ్యము)
- వృత్తం మీది బిందువుల సమితి.(వృత్తము)
- వృత్తం అంతర బిందువుల సమితి.(వృత్త అంతరము)
సర్వ సమాన వృత్తాలు[మార్చు]
రెండు వృత్తాల వ్యాసార్థాలు సమానమైతే ఆ వృత్తాలను సర్వసమాన వృత్తాలు అంటారు.
వృత్త కేంద్రం[మార్చు]
వృత్తము అనునది అనంతమైన బిందువుల సముదాయం. అన్ని బిందువులు ఒక స్థిర బిందువు నుండి సమాన దూరంలో ఉంటాయి. ఆ స్థిర బిందువును వృత్త కేంద్రము అంటారు.
వృత్త వ్యాసార్థము[మార్చు]
వృత్తము పై గల ఏదేని బిందువునుండి వృత్త కేంద్రమునకు గల దూరాన్ని వృత్త వ్యాసార్థం అంటారు. దీనిని ఆంగ్లంలో "radius" అంటారు.వృత్త కేంద్రాన్ని వృత్తం పైని ఏదేని బిందువుతో కలిపే రేఖా ఖండాన్ని ఆ వృత్త వ్యాసార్థం అంటారు.ఒక వృత్తానికి లెక్కలేనన్ని వ్యాసార్థాలు ఉంటాయి.
వృత్త జ్యా[మార్చు]
వృత్తముపై గల ఏవైనా రెండు బిందువులను కలిపే రేఖాఖండమును వృత్త జ్యా అంటారు. ఇది వృత్తాన్ని రెండు వృత్తఖండాలుగా విభజిస్తుంది.వృత్తమునకు గల జ్యాలలో అతి పెద్దదైనది వృత్త వ్యాసము అవుతుంది.వృత్తమునకు జ్యాలు అనేకం ఉంటాయి.
వృత్త వ్యాసము[మార్చు]
ఒక వృత్తంలో కేంద్రంగుండా పోవు జ్యాను వ్యాసము అంటారు. వృత్తము అనగా ఒక సమతలంలో ఒక స్థిర బిందువు నుండి సమాన దూరంలో గల బిందువుల సమితి. వృత్తం పై గల బిందువుల నుండి సమాన దూరంలో గల స్థిర బిందువును కేంద్రము అంటారు. వృత్తం పై ఏవేని రెండు బిందువులను కలిపిన రేఖాఖండమును వృత్త జ్యా(Chord) అంటారు. వృత్తమునకు అనేకజ్యాలు గీయవచ్చు. అన్ని జ్యా లలో కేంద్రం గుండ పోవు జ్యా అతి పెద్ద జ్యా అవుతుంది. దీనిని వ్యాసము అంటారు. వృత్తమున అనంతమైన వ్యాసములు గీయవచ్చు. అన్ని వ్యాసముల కొలతలు సమానంగా ఉంటాయి. వ్యాసమును ఆంగ్లంలో "డయామీటర్"(Diameter) అంటారు. దీన్ని "d"తో సూచిస్తారు.
- వృత్త వ్యాసము వృత్తమును రెండు సర్వ సమాన అర్థ వృత్తములుగా విభజిస్తుంది.
- వృత్త వ్యాసము గుండా పోవు రేఖ వృత్తానికి సౌష్టవాక్షం అవుతుంది. వృత్తానికి అనంతమైన సౌష్టవ రేఖలు గీయవచ్చు.
- వృత్త వ్యాసం పరిధి వద్ద చేయు కోణం 90 డిగ్రీలు లెదా సమకోణం. అనగా వృత్తం పై ఏదేని బిందువుతో వ్యాసం యేర్పరచు త్రిభుజం సమకోణ త్రిభుజం అవుతుంది.
వృత్తం ఏవెని రెండు బిందువులను కలుపు రేఖా ఖండం కేంద్రం గుండా పోతే దానిని వ్యాసం అందురు. వ్యాసంలో సగ భాగమును వ్యాసార్థం లేక అర్థ వ్యాసము అందురు. దీనిని "radius" అంటారు. దీనిని "r"తో సూచిస్తారు.
| వృత్త వ్యాసము = 2(వ్యాసార్థం) Diameter = 2(Radius) |
ఛేదనరేఖ[మార్చు]
వృత్తముపై గల ఏవేని బిందువుల గుండా పోవు రేఖను ఛేదన రేఖ అంటారు.
వృత్త చాపం[మార్చు]
వృత్తములో ఒక భాగాన్ని వృత్త చాపం అంటారు. వృత్తం పై గల ఏవేని బిందువులు వృత్తాన్ని రెండు చాపాలుగా విభజిస్తాయి. ఆ రెండు బిందువులు వ్యాసం యొక్క చివరి బిందువులైతే అవి వృత్తాన్ని రెండు సమాన చాపాలుగా విభజిస్తాయి. ఆ బిందువులు కాకుండా వేరొక బిందువులైతే వృత్తాన్ని లఘు చాపం,గురు చాపంగా విభజిస్తాయి. నిజ జీవితంలో స్త్రీలు చేతికి ధరించే గాజును ముక్కలు చేస్తే యేర్పడిన ముక్కలు చాపాలకు ఉదాహరణ.
వృత్త ఖండం[మార్చు]
వృత్తంలో ఏదేని జ్యా వృత్తాన్ని రెండు వృత్త ఖండాలుగా విభజిస్తుంది. అతి పెద్ద జ్యా అయిన వ్యాసం వృత్తాన్ని రెండు అర్థవృత్తాలుగా విభజిస్తుండి. ఈ అర్థ వృత్తాలు సమాన వృత్త ఖండాలు. వ్యాసం కాని జ్యా వృత్తాన్ని రెండు వృత్త ఖండాలుగా విభజిస్తే రెండు సమానం గాని వృత్త ఖండాలు యెర్పడతాయి. చిన్న ఖండమును లఘు వృత్త ఖండం అని, పెద్ద ఖండమును గురు వృత్త ఖండం అని అంటారు.
సెక్టరు[మార్చు]
వృత్తంలో ఏవేని రెండు వ్యాసార్థాలు, అవి యేర్పరచు వాపం మధ్య ప్రాంతమును "సెక్టరు" అంటారు. రెండు వ్యాసార్థాలు ఒక వ్యాసము పైనవి అయితే వృత్తం యేర్పరిచే రెండు అర్థ వృత్తాలు సమాన సెక్టరు లవుతాయి. రెండు వ్యాసార్థాలు ఒకే వ్యాసము పైనవి కాకపోతే రెండు సమానం కాని సెక్టరులు యేర్పడతాయి. వాటిని లఘు సెక్టరు, గురు సెక్టరు లుగా పిలువ వచ్చు. సెక్టరు యొక్క రెండు వ్యాస్తార్థాలు వృత్త కేంద్రం వద్ద చేయు కోణమును సెక్టరు కోణం అంటారు.
సెక్టరు వైశాల్యం[మార్చు]
వృత్త వ్యాసార్థం "r", సెక్టరు కోణం "x" డిగ్రీలు అయినపుడు ఈ క్రింది సూత్రముతో సెక్టరు వైశాల్యమును గణించవచ్చు.
- సెక్టరు వైశాల్యము = πr2
సెక్టరు చాపము[మార్చు]
వృత్త వ్యాసార్థం "r", సెక్టరు కోణం "x" డిగ్రీలు అయినపుడు ఈ క్రింది సూత్రముతో సెక్టరుచాపమును గణించవచ్చు.
- సెక్టరు చాపము = 2πr
వృత్త వ్యాసము,పరిధి మధ్య సంబంధము[మార్చు]
సాధారణంగా వృత్త పరిధి, వృత్త వ్యాసము మధ్య గల సంబంధం స్థిరంగా ఉంటుంది. దీని విలువ సుమారు 22/7 ఉంటుదని అంచనా.
7 యూనిట్లు వ్యాసము గల వృత్తం యొక్క పరిధి సుమారు 22 యూనిట్లు ఉండును. అదే విధంగా 14 యూనిట్లు వ్యాసము గల వృత్తం యొక్క పరిధి 44 యునిట్లు ఉండును. అందువలన వృత్త పరిధి, వ్యాసము ల నిష్పత్తి ఎల్లపుడూ స్థిరంగా ఉంటుంది. ఈ స్థిర సంఖ్యను గ్రీకు అక్షరమైన ఫై (π) తో సూచిస్తారు. దీని విలువ సుమారు 3.14... ఉంటుంది.
| వృత్త పరిధి / వృత్త వ్యాసము =π వృత్త పరిధి = π(వ్యాసము) |
వృత్త చుట్టుకొలత(వృత్త పరిధి)[మార్చు]

వృత్తము యొక్క మొత్తం పొడవును వృత్తం చుట్టుకొలత లేదా వృత్త పరిధి అంటారు. దీనిని ఆంగ్లంలో "circumference" అంటారు.ఈ పరిధి వృత్త వ్యాసానికి "ఫై" రెట్లుంటుంది.
| వృత్త పరిధి = π(వ్యాసము) వృత పరిధి = 2π(వ్యాసార్థము) |
వృత్త వైశాల్యము[మార్చు]
వృత్తము ఆక్రమించే స్థల పరిమాణాన్ని వృత్త వైశాల్యం అంటారు. దీనిని చదరపు యూనిట్లలో తెలుపుతారు.
వృత్త వైశాల్యమునకు సూత్రం రాబట్టుట[మార్చు]


ఒక వృత్తాకార అట్ట ముక్కను తీసుకొని దాని వ్యాసార్థాల వెంబడి అనేక ముక్కలుగా పటంలో చూపబడినట్లు కత్తిరించాలి. ఆ కత్తిరించిన ముక్కలు సెక్టరు ఆకారంలో ఉంటాయి.మొదటి పటంలో వృత్త పరిధి ఎరుపు రంగుగా చూపబడింది. వ్యాసార్థములు నీలం రంగుగా చూపబడింది. ఈ ముక్కలను తారుమారుచేస్తూ అన్నిముక్కలను పేర్చినట్లయితే అది రెండవ పటంలో చూపబడినట్లు దీర్థ చతురస్రంగా మారుతుంది. యిపుడు మొదటి పటంలో గల వృత్త వైశాల్యము రెండవ పటంలో దీర్ఘచతురస్ర వైశాల్యమునకు సమానమవుతుంది. ఇపుడు దీర్ఘ చతురస్ర పొడవు మొదటి పటంలో గల వృత్త పరిధిలో సగం ఉంటుంది.అనగా పటంలో చూపబడిన ఎరుపు రంగు రేఖ పొడవు 2πr కావున దానిలో సగభాగం πr అగును ఇది దీర్ఘ చతురస్ర పొడవు అగును. అదేవిధంగా దీర్ఘ చతురస్ర వెడల్పు మొదటి పటంలోని వృత్త వ్యాసార్థానికి సమానం. అందువలన దీర్ఘ చతురస్ర వెడల్పు r యూనిట్లు అవుతుంది. దీర్ఘ చతురస్ర వైశాల్యం పొదవు,వెడల్పుల లబ్ధం కావున πr, r ల లబ్ధం πr2 అవుతుంది. ఇది వృత్త వైశాల్యమునకు సమానమవుతుంది.
- మొదటి పటంలోని వృత్త పరిధి రెండుభాగములుగా విభజింపబడింది.
- రెండవ పటంలో దీర్ఘ చతురస్ర పొడవులుగా మొదటి పటంలోని పరిధి మారినది.
- మొదటి పటం లోని వ్యాసార్థం రెండవ పటం లోని దీర్ఘ చతురస్ర వెడల్పుగా మారినది.
- మొదటి పటం లోని వృత్తమునే రేండవ పటంగా అమర్చాము కనుక వృత్త వైశాల్యము = దీర్ఘ చతురస్ర వైశాల్యము అవుతుంది.
- అందువలన వృత్త వైశాల్యము (A)= πr2 అవుతుంది.
| వృత్త వైశాల్యము = π(వ్యాసార్థము)2 A= πr2 |
రేడియన్[మార్చు]
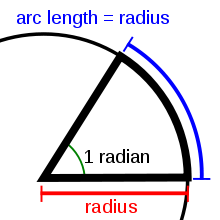
వృత్త వ్యాస్తార్థమునకు సమానమైన వ్యాసార్థం వృత్తకేంద్రం వద్ద చేయు కోణమును రేడియన్ అంటారు. యిది కోణమును సూచించు ప్రమాణం. 360 డిగ్రీలు 2π రేడియన్లకు సమానమవుతుంది.
| 3600 =2π రేడియన్లు 1800 =π రేడియన్లు |
For example:
Conversely, to convert from degrees to radians, multiply by π/180.
For example:
Radians can be converted to turns by dividing the number of radians by 2π.







