అటామిక్ ఆర్బిటాల్

ఎడమ వైపున ఉన్న బొమ్మ శక్తి పెరిగే క్రమంలో కక్ష్యలు చూపిస్తుంది. ఉదాహరణలుగా కుడివైపున కక్ష్య ఆకారాలు ఉన్నాయి.

పరమాణు సిద్ధాంతం, క్వాంటం మెకానిక్స్‌లో, పరమాణు కక్ష్య అనేది ఒక పరమాణువులోని ఎలక్ట్రాన్ స్థానం తరంగ-వంటి ప్రవర్తనను వివరించే గణిత విధి . పరమాణువు కేంద్రకం చుట్టూ ఏదైనా నిర్దిష్ట ప్రాంతంలో ఒక పరమాణువు ఏదైనా ఎలక్ట్రాన్‌ను కనుగొనే సంభావ్యతను గణించడానికి ఈ ఫంక్షన్ ఉపయోగించబడుతుంది . పరమాణు కక్ష్య అనే పదం భౌతిక ప్రాంతాన్ని లేదా కక్ష్య నిర్దిష్ట గణిత రూపం ద్వారా అంచనా వేయబడినట్లుగా, ఎలక్ట్రాన్ ఉన్నట్లు లెక్కించబడే స్థలాన్ని కూడా సూచిస్తుంది.

పరమాణువులోని ప్రతి కక్ష్య మూడు క్వాంటం సంఖ్యల n, ℓ, m l విలువల సమితి ద్వారా వర్గీకరించబడుతుంది, ఇవి వరుసగా ఎలక్ట్రాన్ శక్తి, కోణీయ మొమెంటం కోణీయ మొమెంటం వెక్టార్ కాంపోనెంట్ ( మాగ్నెటిక్ క్వాంటం సంఖ్య ) కి అనుగుణంగా ఉంటాయి. మాగ్నెటిక్ క్వాంటం సంఖ్యకు ప్రత్యామ్నాయంగా, కక్ష్యలు తరచుగా అనుబంధిత హార్మోనిక్ బహుపదిలచే లేబుల్ చేయబడతాయి (ఉదా xy, x 2 - y 2 ). అటువంటి ప్రతి కక్ష్యను గరిష్ఠంగా రెండు ఎలక్ట్రాన్లు ఆక్రమించవచ్చు, ప్రతి ఒక్కటి దాని స్వంత ప్రొజెక్షన్ స్పిన్‌తో ఉంటుంది . సాధారణ పేర్లు s కక్ష్య, p కక్ష్య, d కక్ష్య,, f కక్ష్య వరుసగా కోణీయ మొమెంటం క్వాంటం సంఖ్య ℓ = 0, 1, 2, 3 కలిగిన కక్ష్యలను సూచిస్తాయి. ఈ పేర్లు, n విలువతో కలిసి, పరమాణువుల ఎలక్ట్రాన్ కాన్ఫిగరేషన్‌లను వివరించడానికి ఉపయోగించబడతాయి . అవి s హార్ప్, p రిన్సిపల్, d, f నిర్దిష్ట శ్రేణి ఆల్కలీ మెటల్ స్పెక్ట్రోస్కోపిక్ లైన్ల యొక్క ప్రారంభ స్పెక్ట్రోస్కోపిస్టుల వివరణ నుండి తీసుకోబడ్డాయి..

పరమాణు కక్ష్యలు పరమాణు కక్ష్య నమూనా యొక్క ప్రాథమిక బిల్డింగ్ బ్లాక్‌లు (ప్రత్యామ్నాయంగా ఎలక్ట్రాన్ క్లౌడ్ లేదా వేవ్ మెకానిక్స్ మోడల్ అని పిలుస్తారు), పదార్థంలో ఎలక్ట్రాన్‌ల సబ్‌మైక్రోస్కోపిక్ ప్రవర్తనను దృశ్యమానం చేయడానికి ఒక ఆధునిక ఫ్రేమ్‌వర్క్. ఈ నమూనాలో బహుళ-ఎలక్ట్రాన్ పరమాణువు యొక్క ఎలక్ట్రాన్ క్లౌడ్ సాధారణ హైడ్రోజన్-వంటి పరమాణు కక్ష్యల ఉత్పత్తి అయిన ఎలక్ట్రాన్ కాన్ఫిగరేషన్‌లో నిర్మించబడినట్లు (సుమారుగా) చూడవచ్చు. ఆవర్తన పట్టికలోని విభాగాలలోని 2, 6, 10, 14 మూలకాల బ్లాక్‌ల పునరావృత ఆవర్తన సహజంగా s, p, d,, పూర్తి సెట్‌ను ఆక్రమించే మొత్తం ఎలక్ట్రాన్‌ల సంఖ్య నుండి పుడుతుంది.f పరమాణు కక్ష్యలు, వరుసగా, అయితే క్వాంటం సంఖ్య n యొక్క అధిక విలువల కోసం, ప్రత్యేకించి ప్రశ్నలోని పరమాణువు ధనాత్మక చార్జ్‌ని కలిగి ఉన్నప్పుడు, కొన్ని ఉప-షెల్స్ యొక్క శక్తులు చాలా సారూప్యంగా మారతాయి, అందువల్ల అవి జనావాసంగా చెప్పబడే క్రమం ఎలక్ట్రాన్లు (ఉదా Cr = [Ar]4s 1 3d 5, Cr 2+ = [Ar]3d 4 ) కొంతవరకు ఏకపక్షంగా మాత్రమే హేతుబద్ధీకరించబడతాయి ఎలక్ట్రాను తత్త్వాన్ని అవగాహన చేసుకోడానికి భౌతిక శాస్త్రంలో అనేక నమూనాలు వాడుకలో ఉన్నాయి. వీటిలో అందరికీ పరిచయమైనది బోర్ నమూనా (Bohr Model). ఈ నమూనాలో సూర్యుడి చుట్టూ గ్రహాలు ఎలా తిరుగుతున్నాయో అదే విధంగా కేంద్రకం (nucleus) చుట్టూ ఎలెక్ట్రాన్లు తిరుగుతూన్నట్లు ఊహించుకుంటాం. ఈ నమూనా కొంత వరకు పనిచేస్తుంది. కానీ, ఎలక్ట్రాను తత్త్వాన్ని పరిపూర్ణంగా వర్ణించదు. నిజానికి ఎలెక్ట్రాను రేణువు (particle) లా ఉండదు, ఒక నిలకడ తరంగం (standing wave) లా ఉంటుందని మరొక నమూనా ఉంది. నిజానికి ఎలక్ట్రాను రేణువు లాగా ఉండదు, నిలకడ తరంగంలాగా ఉండదు, రెండు లక్షణాలు ఒకే సారి ప్రవర్తిస్తూ ఉంటుందని ఇప్పటి అవగాహన!

ఎలక్ట్రాన్ లక్షణాలు

• ఎలక్ట్రానులు సూర్యుడి చుట్టూ గ్రహాలు మాదిరి తిరగవు. నిజానికి ఎలక్టానులు నిలకడ తరంగాలులా ఉంటాయి. ఒక ఎలక్ట్రాను తన కనిష్ఠ శక్తి స్థానం (lowest energy state) లో ఉన్నప్పుడు వీణ అది తీగని మీటినప్పుడు పుట్టే ప్రాథమిక తరంగం (fundamental frequency) లాంటి స్థితిలో ఉంటుంది.
• ఎలక్ట్రాను ఫలానా చోట అంటూ ఎక్కడా ఉండదు; అంతటా ఉంటుంది. అది ఒక నిర్ధిష్ఠ స్థానంలో ఎంత సంభావ్యతతో ఉంటుందో తరంగ ప్రమేయం (wave function) సహాయంతో లెక్క కట్టి చెప్పవచ్చు.
• ఒక కేంద్రకం చుట్టూ ఉండే ఎలక్ట్రానులు ఎల్లప్పుడు పూర్ణ సంఖ్యలోనే ఉంటాయి; అర ఎలక్ట్రానులు, పావు ఎలక్ట్రానులు ఉండవు.
• ఒక శక్తి స్థానం నుండి మరొక శక్తి స్థానానికి గెంతేటప్పుడు ఎలక్ట్రానులు ఎల్లప్పుడు పూర్ణ సంఖ్యలోనే గెంతుతాయి.
• ఎలక్ట్రానులు ఎల్లప్పుడు కొన్ని రేణువు లక్షణాలని పోగొట్టుకోవు. ఉదాహరణకి ఎలక్ట్రాను ఏ శక్తి స్థానంలో ఉన్నా దాని ఉత్తేజితం (charge) ఒక్కటే. అలాగే ఎలక్ట్రాను ఏ శక్తి స్థానంలో ఉన్నా దాని తిరుగుడు (spin) విలువ మారదు.

ఇప్పుడు ఆర్బిటాల్ అంటే ఏమిటో అర్థం చేసుకుందాం. ఇంగ్లీషులోని ఆర్బిట్‌ (orbit) అన్న మాటని తెలుగులో కక్ష్య అంటారు. ఉదాహరణకి సూర్యుడు చుట్టూ భూమి తిరిగే మార్గాన్ని కక్క్ష్య అంటారు. కాని ఎలక్ట్రాను కేంద్రకం చుట్టూ ఒక కక్ష్యలో తిరగదు. (బోర్ అలా తిరుగుతుందని అనుకున్నాడు కాని అది నిజం కాదు.) ఎలక్ట్రాను కేంద్రకం చుట్టూ ఒక గుండ్రటి కెరటంలా ఉంటుంది. అనగా ఒక బంతిలా ఒక చోట కాకుండా కేంద్రకం చుట్టూ అలికేసినట్లు ఉంటుంది. ఈ అలికేసిన ప్రాంతం స్థిరంగా ఒక సిబ్బిలా కాకుండా పైకీ, కిందికీ ఊగిసలాడుతూ ఉంటుంది. ఇది రకరకాల ఆకారాలలో ఊగిసలాడుటతూ ఉంటుంది. ఈ ఆకారాలని వర్ణించడానికి ఇంగ్లీషులో "ఆర్బిటల్" (orbital) అన్న మాట వాడతారు. దీనిని తెలుగులో "ఊగిసలాడే కెరటం" అనొచ్చు లేదా టూకీగా కెరటకం అనొచ్చు లేదా ఆర్బిటల్ అన్న ఇంగ్లీషు మాట వాడేసుకోవచ్చు. అధికారిక క్వాంటం మెకానికల్ భాషలో పరమాణు కక్ష్యలను మరింత కచ్చితంగా నిర్వచించవచ్చు . అవి పరమాణు కేంద్రకం యొక్క విద్యుత్ క్షేత్రం ద్వారా పరమాణువుకు కట్టుబడి ఉండే ఎలక్ట్రాన్ల కోసం ష్రోడింగర్ సమీకరణానికి సుమారుగా పరిష్కారాలు . ప్రత్యేకించి, క్వాంటం మెకానిక్స్‌లో, పరమాణువు యొక్క స్థితి, అనగా, పరమాణు హామిల్టోనియన్ యొక్క ఈజెన్‌స్టేట్, ఒక విస్తరణ ద్వారా అంచనా వేయబడుతుంది ( కాన్ఫిగరేషన్ ఇంటరాక్షన్ ఎక్స్‌పాన్షన్, బేస్ సెట్ చూడండి ) యాంటీ-సిమెట్రైజ్డ్ ఉత్పత్తుల ( స్లేటర్ డిటర్మినెంట్స్ ) యొక్క లీనియర్ కాంబినేషన్‌గా) ఒక-ఎలక్ట్రాన్ ఫంక్షన్ల. ఈ ఒక-ఎలక్ట్రాన్ ఫంక్షన్ల యొక్క ప్రాదేశిక భాగాలను అటామిక్ ఆర్బిటాల్స్ అంటారు. (వాటి స్పిన్ కాంపోనెంట్‌ను కూడా పరిగణనలోకి తీసుకున్నప్పుడు, అటామిక్ స్పిన్ ఆర్బిటాల్స్ గురించి మాట్లాడతారు .) ఒక స్థితి వాస్తవానికి అన్ని ఎలక్ట్రాన్‌ల కోఆర్డినేట్‌ల ఫంక్షన్, తద్వారా వాటి కదలిక పరస్పర సంబంధం కలిగి ఉంటుంది, అయితే ఇది తరచుగా ఈ స్వతంత్ర-కణ నమూనా ద్వారా అంచనా వేయబడుతుంది. సింగిల్ ఎలక్ట్రాన్ వేవ్ ఫంక్షన్ల ఉత్పత్తులు. [8] ( ఉదాహరణకు, లండన్ డిస్పర్షన్ ఫోర్స్, ఎలక్ట్రాన్ల కదలిక యొక్క పరస్పర సంబంధాలపై ఆధారపడి ఉంటుంది.) పరమాణు భౌతిక శాస్త్రంలో, పరమాణు వర్ణపట రేఖలు అణువు యొక్క క్వాంటం స్థితుల మధ్య పరివర్తనలకు ( క్వాంటం లీప్స్ ) అనుగుణంగా ఉంటాయి. ఈ స్థితులు టర్మ్ సింబల్‌లో సంగ్రహించబడిన క్వాంటం సంఖ్యల సెట్ ద్వారా లేబుల్ చేయబడతాయి, సాధారణంగా నిర్దిష్ట ఎలక్ట్రాన్ కాన్ఫిగరేషన్‌లతో అనుబంధించబడతాయి, అనగా, పరమాణు కక్ష్యల యొక్క ఆక్యుపేషన్ స్కీమ్‌ల ద్వారా (ఉదాహరణకు, నియాన్ - టర్మ్ సింబల్ యొక్క గ్రౌండ్ స్టేట్ కోసం 1s 2 2s 2 2p 6 : 1 S 0 ). కాన్ఫిగరేషన్ ఇంటరాక్షన్ విస్తరణలో సంబంధిత స్లేటర్ డిటర్మినెంట్‌లు స్పష్టమైన అధిక బరువును కలిగి ఉన్నాయని ఈ సంజ్ఞామానం అర్థం . పరమాణు కక్ష్య భావన అనేది ఇచ్చిన పరివర్తనతో అనుబంధించబడిన ఉత్తేజిత ప్రక్రియను దృశ్యమానం చేయడానికి కీలకమైన భావన . ఉదాహరణకు, ఇచ్చిన పరివర్తన కోసం అది ఆక్రమిత కక్ష్య నుండి ఇచ్చిన ఖాళీ కక్ష్యకు ఎలక్ట్రాన్ యొక్క ఉత్తేజానికి అనుగుణంగా ఉంటుందని చెప్పవచ్చు. ఏదేమైనా, ఎలక్ట్రాన్లు పౌలీ మినహాయింపు సూత్రం ద్వారా పాలించబడే ఫెర్మియన్లు, ఒకదానికొకటి వేరు చేయలేవని గుర్తుంచుకోవాలి. అంతేకాకుండా, కాన్ఫిగరేషన్ ఇంటరాక్షన్ విస్తరణ చాలా నెమ్మదిగా కలుస్తుంది, సాధారణ వన్-డిటర్మినెంట్ వేవ్ ఫంక్షన్ గురించి మాట్లాడలేము. ఎలక్ట్రాన్ సహసంబంధం పెద్దగా ఉన్నప్పుడు ఇది జరుగుతుంది . ప్రాథమికంగా, పరమాణు కక్ష్య అనేది ఒక-ఎలక్ట్రాన్ వేవ్ ఫంక్షన్, అయినప్పటికీ చాలా ఎలక్ట్రాన్లు ఒక-ఎలక్ట్రాన్ పరమాణువులలో లేనప్పటికీ, ఒక-ఎలక్ట్రాన్ వీక్షణ ఉజ్జాయింపుగా ఉంటుంది. కక్ష్యల గురించి ఆలోచిస్తున్నప్పుడు, పరమాణు కక్ష్య సిద్ధాంతం యొక్క సంక్లిష్టతలను తగ్గించడానికి ఇది ఒక మార్గం అయిన హార్ట్రీ-ఫాక్ ఉజ్జాయింపు ద్వారా ఎక్కువగా ప్రభావితమయ్యే కక్ష్య విజువలైజేషన్‌ని మేము తరచుగా అందిస్తాము .

ఆర్బిటాల్స్ రకాలు

పరమాణు కక్ష్యలు హైడ్రోజన్-వంటి "కక్ష్యలు" కావచ్చు, ఇవి హైడ్రోజన్-వంటి "అణువు" (అంటే, ఒక ఎలక్ట్రాన్‌తో కూడిన అణువు) కోసం ష్రోడింగర్ సమీకరణానికి కచ్చితమైన పరిష్కారాలు. ప్రత్యామ్నాయంగా, పరమాణు కక్ష్యలు ఒక ఎలక్ట్రాన్ యొక్క కోఆర్డినేట్‌లపై ఆధారపడి ఉండే ఫంక్షన్‌లను సూచిస్తాయి (అంటే, ఆర్బిటాల్స్) కానీ అణువు లేదా అణువులోని అన్ని ఎలక్ట్రాన్‌ల ఏకకాల కోఆర్డినేట్‌లపై ఆధారపడి ఉండే వేవ్ ఫంక్షన్‌లను అంచనా వేయడానికి ప్రారంభ బిందువులుగా ఉపయోగిస్తారు. పరమాణు కక్ష్యల కోసం ఎంచుకున్న కోఆర్డినేట్ వ్యవస్థలు సాధారణంగా అణువులలోని గోళాకార కోఆర్డినేట్‌లు ( r,  θ,  φ ), కార్టేసియన్ ( x,  y,  z ) ) పాలిటామిక్ అణువులలో. గోళాకార కోఆర్డినేట్‌ల (అణువుల కోసం) ప్రయోజనం ఏమిటంటే, కక్ష్య తరంగ పనితీరు మూడు కారకాల యొక్క ఉత్పత్తి, ఒక్కొక్కటి ఒకే కోఆర్డినేట్‌పై ఆధారపడి ఉంటుంది:

చరిత్ర

"కక్ష్య" అనే పదాన్ని రాబర్ట్ ముల్లికెన్ 1932లో వన్-ఎలక్ట్రాన్ ఆర్బిటల్ వేవ్ ఫంక్షన్‌కు సంక్షిప్తంగా రూపొందించారు . ఏది ఏమైనప్పటికీ, ఎలక్ట్రాన్లు కచ్చితమైన కోణీయ మొమెంటం కలిగిన కాంపాక్ట్ న్యూక్లియస్ చుట్టూ తిరుగుతాయనే ఆలోచనను కనీసం 19 సంవత్సరాల క్రితం నీల్స్ బోర్ వాదించారు,, జపనీస్ భౌతిక శాస్త్రవేత్త హంటారో నగోకా ఎలక్ట్రానిక్ ప్రవర్తన కోసం ఒక కక్ష్య-ఆధారిత పరికల్పనను ప్రచురించారు. 1904 నాటికే. ఈ ఎలక్ట్రాన్ "కక్ష్యల" ప్రవర్తనను వివరించడం క్వాంటం మెకానిక్స్ అభివృద్ధి వెనుక ఉన్న చోదక శక్తులలో ఒకటి .

ప్రారంభ నమూనాలు

1897 లో JJ థామ్సన్ ఎలక్ట్రాన్‌ను కనుగొనడంతో, పరమాణువులు ప్రకృతి యొక్క అతి చిన్న బిల్డింగ్ బ్లాక్‌లు కాదని, అవి మిశ్రమ కణాలు అని స్పష్టమైంది. పరమాణువులలో కొత్తగా కనుగొనబడిన నిర్మాణం, పరమాణువు భాగాలు ఒకదానితో ఒకటి ఎలా సంకర్షణ చెందుతాయో ఊహించడానికి చాలా మందిని ప్రేరేపించాయి. థామ్సన్ ధనాత్మకంగా చార్జ్ చేయబడిన జెల్లీ-వంటి పదార్ధం లోపల కక్ష్య-వంటి రింగులలో బహుళ ఎలక్ట్రాన్లు తిరుగుతాయని సిద్ధాంతీకరించారు, ఎలక్ట్రాన్ ఆవిష్కరణ 1909 మధ్య, ఈ " ప్లమ్ పుడ్డింగ్ మోడల్ " పరమాణు నిర్మాణం అత్యంత విస్తృతంగా ఆమోదించబడిన వివరణ. థామ్సన్ కనుగొన్న కొద్దికాలానికే, హంటారో నగోకా ఎలక్ట్రానిక్ నిర్మాణానికి భిన్నమైన నమూనాను అంచనా వేశారు. ప్లం పుడ్డింగ్ మోడల్‌లా కాకుండా, నాగోకా "సాటర్నియన్ మోడల్"లోని ధనాత్మక చార్జ్ కేంద్ర కోర్‌లో కేంద్రీకృతమై, ఎలక్ట్రాన్‌లను శని వలయాలను గుర్తుకు తెచ్చే వృత్తాకార కక్ష్యలోకి లాగుతుంది. ఆ సమయంలో కొంతమంది వ్యక్తులు నగోకా పనిని గమనించారు, నగావోకా స్వయంగా దాని భావనలో కూడా సిద్ధాంతంలో ఒక ప్రాథమిక లోపాన్ని గుర్తించాడు, అనగా క్లాసికల్ చార్జ్డ్ వస్తువు కక్ష్య కదలికను కొనసాగించదు ఎందుకంటే అది వేగవంతం అవుతుంది, విద్యుదయస్కాంతం కారణంగా శక్తిని కోల్పోతుంది. రేడియేషన్. అయినప్పటికీ, సాటర్నియన్ మోడల్ఆధునిక సిద్ధాంతంతో దాని సమకాలీనుల కంటే ఎక్కువ ఉమ్మడిగా ఉన్నట్లు తేలింది.

బోర్ అణువు

1909లో, ఎర్నెస్ట్ రూథర్‌ఫోర్డ్ పరమాణు ద్రవ్యరాశిలో ఎక్కువ భాగం కేంద్రకంలోకి గట్టిగా ఘనీభవించబడిందని కనుగొన్నాడు, అది కూడా ధనాత్మక చార్జ్‌తో ఉన్నట్లు కనుగొనబడింది. ప్లం పుడ్డింగ్ మోడల్ పరమాణు నిర్మాణాన్ని వివరించలేకపోయిందని 1911లో అతని విశ్లేషణ ద్వారా స్పష్టమైంది. 1913లో, రూథర్‌ఫోర్డ్ పోస్ట్-డాక్టోరల్ విద్యార్థి, నీల్స్ బోర్, పరమాణువు యొక్క ఒక కొత్త నమూనాను ప్రతిపాదించాడు, దీనిలో ఎలక్ట్రాన్లు శాస్త్రీయ కాలాలతో కేంద్రకం చుట్టూ పరిభ్రమిస్తాయి, కానీ కోణీయ మొమెంటం యొక్క వివిక్త విలువలను మాత్రమే h /2π యూనిట్లలో పరిమాణీకరించడానికి అనుమతించబడ్డాయి . ఈ పరిమితి ఎలక్ట్రాన్ శక్తుల యొక్క నిర్దిష్ట విలువలను మాత్రమే స్వయంచాలకంగా అనుమతించింది. బోర్ మోడల్పరమాణువు భూమి స్థితి నుండి రేడియేషన్ నుండి శక్తిని కోల్పోయే సమస్యను పరిష్కరించింది (దీనికి దిగువన ఎటువంటి స్థితి లేదని ప్రకటించడం ద్వారా), మరింత ముఖ్యంగా వర్ణపట రేఖల మూలాన్ని వివరించింది. ఉద్గార కాంతి తరంగదైర్ఘ్యంతో అణువులలోని శక్తి స్థాయిలను అనుసంధానించడానికి ఫోటోఎలెక్ట్రిక్ ప్రభావం గురించి బోర్ ఐన్‌స్టీన్ వివరణను ఉపయోగించిన తర్వాత, అణువులలోని ఎలక్ట్రాన్ల నిర్మాణం అణువుల ఉద్గార, శోషణ వర్ణపటం మధ్య అనుసంధానం అవగాహనలో మరింత ఉపయోగకరమైన సాధనంగా మారింది. అణువులలోని ఎలక్ట్రాన్ల. ఉద్గార శోషణ స్పెక్ట్రా (19వ శతాబ్దం మధ్యకాలం నుండి ప్రయోగాత్మకంగా తెలిసినది) అత్యంత ప్రముఖమైన లక్షణం ఏమిటంటే, ఈ పరమాణు వర్ణపటంలో వివిక్త రేఖలు ఉంటాయి. బోర్ నమూనా ప్రాముఖ్యత ఏమిటంటే, ఎలక్ట్రాన్లు అణువు చుట్టూ పట్టే కక్ష్యల మధ్య శక్తి వ్యత్యాసాలకు ఉద్గార శోషణ స్పెక్ట్రాలోని పంక్తులకు సంబంధించింది. కాదు ఎలక్ట్రాన్‌లకు కొన్ని రకాల తరంగ-వంటి లక్షణాలను ఇవ్వడం ద్వారా బోర్ సాధించాడు, బొమ్మ చూడండి.

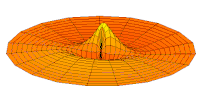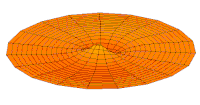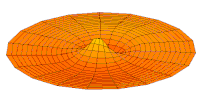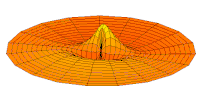
• s-type drum modes and wave functions
• 
  Drum mode $u_{01}$
• 
  Drum mode $u_{02}$
• 
  Drum mode $u_{03}$
• 
  Wave function of 1s orbital (real part, 2D-cut, $r_{max}=2a_{0}$)
• 
  Wave function of 2s orbital (real part, 2D-cut, $r_{max}=10a_{0}$)
• 
  Wave function of 3s orbital (real part, 2D-cut, $r_{max}=20a_{0}$)

• p-type drum modes and wave functions
• 
  Drum mode $u_{11}$
• 
  Drum mode $u_{12}$
• 
  Drum mode $u_{13}$
• 
  Wave function of 2p orbital (real part, 2D-cut, $r_{max}=10a_{0}$)
• 
  Wave function of 3p orbital (real part, 2D-cut, $r_{max}=20a_{0}$)
• 
  Wave function of 4p orbital (real part, 2D-cut, $r_{max}=25a_{0}$)

• d-type drum modes
• 
  Mode $u_{21}$ (3d orbital)
• 
  Mode $u_{22}$ (4d orbital)
• 
  Mode $u_{23}$ (5d orbital)

ఇది చాల క్లిష్టమైన ఊహనం. గణితం సహాయం లేకుండా గభీమని అర్థం కాదు. ఆధునిక గుళిక శాస్త్రం (modern quantum mechanics) కక్ష్యలు (orbits) వాడరు; ఆ స్థానంలో కెరటకాలు (orbitals) వాడతారు.